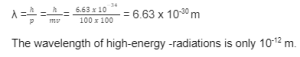A de Broglie wave, also known as a matter wave, is any feature of a material object’s activity or qualities that fluctuates in time or space in accordance with the mathematical equations that determine waves. The French physicist Louis de Broglie proposed that particles could have wave properties attributed to particle properties, based on the wave and particle behavior of light, which had already been demonstrated experimentally. The wave character of electrons was discovered experimentally three years later. The calculated wavelength of daily items, on the other hand, is considerably smaller than those of electrons, thus their wave qualities have never been identified; familiar objects only exhibit particle behavior. Only in the real of subatomic particles do De Broglie waves play an important role.
Only when the standing waves fit uniformly around the loop can De Broglie waves around with a closed system, such as those related with electrons circling nuclei in atoms, persist; otherwise, they cancel out. As a result of this need, electrons in atoms choose only a few configurations, or states, out of the many which would otherwise be accessible.
The response of a particle’s wave characteristics to an external force is governed by a fundamental law of quantum mechanics known as the Schrödinger equation in its mathematical form.
wave nature of matter
Among the most perplexing concepts in physics is the wave aspect of matter. You’ve seen examples of light that would be both particles and waves in nature. Because of Albert Einstein’s generosity, you are aware of the Photoelectric Effect.
In the photoelectric effect, electrons and photons have particle-like characteristics, similar to a billiard ball. However, you are also most likely familiar with the Diffraction experiment and the Interference Rings.
Similar to how two waves on a pond’s surface contact. In these examples, we can see how light behaves as a wave. It’s a fascinating puzzle. It even has something to do with our vision. The eye-lens’ light collecting and focussing mechanism follows the wave characteristic of light. However, its absorption by the retina’s rods and cones is consistent with light’s particle nature. As we were still trying to figure out what was going on, Louis de Broglie arrived to add to the confusion with his de Broglie Relation.
de Broglie Equation
One of its equations widely used to define the wave characteristics of matter is the de Broglie equation. It essentially explains the electron’s wave nature.
Electromagnetic radiation has the properties of both a particle (with momentum) and a wave (expressed in frequency, wavelength). This dual nature trait was also discovered in microscopic particle-like electrons.In his thesis, Louis de Broglie proposed that each moving particle, either microscopic or macroscopic, has a wave character. ‘Matter Waves’ was the title. He also proposed a relationship between a particle’s velocity and momentum and its wavelength if the particle had to act like a wave.
However, the particle and wave natures of matter appeared to be incompatible, as neither property could be demonstrated in a single experiment. It’s because every experiment is usually founded on a concept, and the outcomes of that principle are only reflected in that experiment and not in others.
Nevertheless, both qualities are required to fully comprehend or characterize the substance. As a result, the particle and wave nature of matter are truly ‘complimentary.’ It is not, however, required that both be present at the same moment. The de Broglie relation is significant because it is more beneficial for small, fundamental particles such as electrons.
For an electron, de Broglie wavelength equation is:
λ = hmv
Here, λ points to the wave of the electron
The electron’s mass is M
The electron’s velocity is denoted by V
Mv is the amount of momentum that is created as a result of this.
This equation was discovered to work for all forms of matter in the cosmos, i.e., everything else in the universe, from living creatures to inanimate objects, has wave particle duality.
de Broglie relation derivation
With the use of the Plank equation, Einstein’s mass energy relation, and the Plank equation of matter, de Broglie proposed the wavelength equation. The smaller the light quanta, the lesser the mass of the photon, according to Einstein’s mass energy equation.If the wavelength of light = λ, frequency = v, and energy = E.
From Planck equation, E = hν = h ⁄ λc
where c = velocity of light
h = Planck constant = 6.627× 10-27
Theory of relativity from Einstein
E = m c2.
Combining these two relations,
mc = h ⁄ λ
or, p =h ⁄ λ
where p = mc = mv = momentum.
∴ Wavelength (λ) = h /p
The de Broglie relation was used to compute the mass, velocity, wavelength frequency, and energy of an electron by extending the light particle to the dynamical particles of matter.
λ = h ⁄ p=h ⁄ mv
where m = total mass of electron
v = velocity.
Conclusion:
De Broglie waves explain the presence of subatomic particles in unusual places because their waves permeate boundaries in the same way that sound does. As a result, in a process known as alpha decay, a hefty atomic nucleus might occasionally release a piece of itself. As a particle, the piece of nucleus (alpha particle) lacks enough energy to overcome the force barrier around the nucleus; however, as a wave, it can get past the barrier—that is, this has a finite chance of being located outside the nucleus.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out