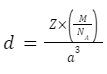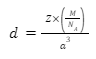The component particles of crystalline solids have a distinct three-dimensional configuration. The relative locations of these particles in the crystal are commonly depicted by points. A space lattice is the arrangement of these unendurable groupings of points. The collar lattice points or lattice sites are the places inhabited by atoms, ions, or molecules in a crystal lattice.
Unit cell
Crystal structure is a depiction of the orderly organisation of atoms, ions, or molecules in a crystalline substance used in crystallography. The symmetry patterns that recur in the major directions of three-dimensional space in matter are caused by the inherent nature of the component particles, resulting in ordered structures.
The smallest collection of particles in the material that makes up this repeating pattern is the structure’s unit cell. The unit cell reflects the complete crystal’s symmetry and structure, which is built up via repeated translation of the unit cell along its fundamental axes.
Types of unit cells
Unit cells may be generically classified into two types:
Primitive unit cell — Constituent particles are only present at the unit cell’s corners in primitive unit cells, whereas one or more constituent particles are present at sites other than the corners in concentrated unit cells.
Centred unit cell– Body-centred unit cell (BCC), face-centred unit cell (FCC), and end-centred unit cell are the three types of centred unit cell (ECC).
Primitive unit cell
Simple unit cells, also known as primitive unit cells, are cells in which the component particles are only present at the corners.
Body Centred Cubic cell
Within the body of the unit cell, one particle is present in contrast to the particles at the corners. A body-centred unit cell is what it’s called.
Face Centred Cubic cell
A face-centred unit cell is one in which the particles are present in the corners and in the centre of each face of the unit cell.
End Centred Cubic cell
End-face centred means that there are particles in the centre of any two opposed faces in addition to the particles at the corners.
Density of Unit cell
A unit cell’s density is defined as the ratio of its mass to its volume.
The mass of the unit cell can be calculated by multiplying the total number of atoms present in the unit cell and the mass of each atom.
So, the mass of the unit cell can be written as: Mass=Z×m
Here, Z is the atomic number and m is the mass of the atoms.
The mass of the atoms present in the unit cell will be calculated as:
m=M/NA
Here, M is the molar mass and NA is Avogadro’s number.
If we assume the edge length of the cubic cell to be a then the volume of the unit cell would be: a³.
Therefore, the formula for the density of the unit cell would be:
d=Zm/a³
Density of primitive unit cells
The number of atoms in a primitive unit cell, z, is equal to one. As a result, density is expressed as:
d=M/a³NA
Density of Body Centred Cubic unit cell
In a Body Centred Cubic unit cell, there are two atoms. As a result, the density may be expressed as-
d=2M/a³NA
Density of Face Centred Cubic unit cell
In a face-centred cubic unit cell, there are four atoms. As a result, the density may be expressed as-
d=4M/a³NA
Density of End Centred Cubic unit cell
In an End-centred cubic unit cell, there are two atoms. As a result, the density may be expressed as-
d=2m/a³NA
Conclusion
We looked at the density of a unit cell, its SI unit, and how it’s calculated in this article. We also looked at how the density of unit cells varied depending on the case: primitive unit cells, body-centred unit cells, face-centred and end centred unit cells. We now know that the density formula for various unit cells is dependent on the number of atoms in the unit cell.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out