Profile
Settings
Refer your friends
Sign out
Young’s Modulus of Elasticity is a numerical constant with the same dimensions as stress (as strain is dimensionless) and is named after the 18th century English Physicist, Thomas Young.
Definition of Young’s modulus of elasticity
Young’s modulus of elasticity is a measure of a material’s ability to resist changes (deformation) when an external force (either a tension or a compression) is applied to it. It is also referred to as the modulus of elasticity and simply put, it is the longitudinal stress divided by the strain.
Denoted by the symbol Y or E, it is also referred to as the modulus of elasticity.
Hooke’s Law and its relation to Young’s modulus of elasticity
Hooke’s law simply states that as long as the material is within its elastic limit, the strain is directly proportional to the stress applied.
Stress ∝ Strain
Thus,
σ ∝ ϵ
σ = Y×ϵ
F/A = Y×(Δl/l) ……….. (1)
Where, Y is a constant of proportionality called Young’s modulus of elasticity or elastic modulus.
F is applied force,
A is the area on which force F is applied,
l is the original length,
Δl is the change in length due to applied force.
Since strain is dimensionless, Young’s modulus of elasticity has the same dimensions as stress.
Let’s understand this with an example:
Take a metal cylinder that has a cross-sectional area of ‘A’ square metres. Now, let this cylinder be pulled with a force with a magnitude ‘F’ at both ends.
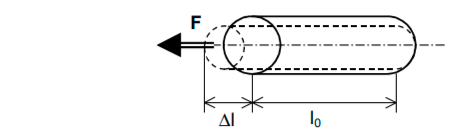
Let the original length of the metal cylinder be l0 and when the forces are applied, let the new elongated length of the cylinder be ln.
Note that as the length of the cylinder increases to ln, the cross-sectional area does not remain ‘A’ as it decreases.
Now, the stress developed in the metal cylinder because of the applied force is:
σ = F/A
And, the elongation produced in the cylinder is:
Δl = ln – l0
Thus, the strain is:
ε = Δl/l0
ε = (ln – l0)/l0
Thus, from equation (1)
F/A = Y×(Δl /l)
Y = (F×l)/(A×Δl)
The derived equation is a form of Hooke’s law. Young’s modulus of elasticity has units as that of stress, as strain is a dimensionless quantity. The units are Newton per metre square in the SI system.
Practical applications of Young’s modulus of elasticity make sense only with the elastic limits of the material. That is, according to the stress-strain curve, when stress is proportional to the strain, (a straight line in the stress-strain curve diagram) because once the material goes beyond this limit, it may have permanent deformation and will not return to its original dimensions.
Some common tests to determine Young’s modulus of elasticity are:
- The tension (or compression) test
- Bending test
- Natural frequency vibration test
Hooke’s law forms the basis of the tension and the bending tests. Together they are called static methods.
Here are values of Young’s modulus of elasticity for some materials:
Other elasticity modulus
Apart from Young’s Modulus of Elasticity, there are two other kinds:
Bulk modulus: The ratio of volumetric stress to volumetric strain
Rigidity modulus: The ratio of shearing stress to shearing strain
Conclusion
Young’s modulus of elasticity determines how stiff a material is. This has important implications when it comes to designing structures, vehicles and in other areas of applied engineering.
Take, for example, the offices that we work in. A particular floor of this office is supported by steel beams that hold the floor. These beams carry loads (weight) of equipment, people and other objects on the floors. Depending on the weight carried, these beams can start deflecting, and thus it is critical to manage this deflection of beams and ensure that these beams deform elastically. So when the beams deflect, they must go back to their original positions.
