Profile
Settings
Refer your friends
Sign out
INTRODUCTION
The ideal gas equation, which also goes by the name ideal gas law, is simply an equation for the state of an ideal gas in a hypothetical situation. This law or equation has its fair share of limitations; still, it provides a good source and approximates the behaviour under various circumstances. This law was a creation and stated in 1834 by Benoit Paul Émile Clapeyron. This equation combined Charles law, Boyles law, Avogadro’s law, and Gay-Lussac’s law. The ideal gas equations define that most real gases, particularly at low pressure, do not give a necessarily better result when pressure is high.
Kinetic Theory and Ideal Gases
Almost every gas is based on an assumption based on the Kinetic Theory of Matter. This theory assumes that all the matter in the world is composed of particles and that there are some spaces between the particles. These particles are specifically atoms or molecules. The attractive forces between become strong, and particles merge. Particles are a constant gas entity that moves randomly and collides with one another and the container walls in which they are incorporated. Each of the molecules inside has some kinetic energy solely dependent on the temperature factor.
An ideal gas is considered so when the particles are in a far distance such that they cannot exert or apply their forces attraction on one another. As of in the real-life timeline, there is no presence of a true ideal gas. In high low pressure and high-temperature conditions, gas behaviour comes close to becoming ideal and obeying the ideal gas equation. This is why the Ideal Gas Law is widely used and is appropriate. Ideal Gas Law pertains to the basic equation being PV = nRt, and values for R being 0.0821, 8.31, and 62.4.
Ideal Gas Equation
The ideal gas equation states that the product of pressure and volume for one gram molecule in an ideal gas is equal to the product of terms comprising Absolute temperature and universal gas constant.
The Ideal gas equation goes by:
PV=nRT
The quantities and variables about this equation are as follows:
Pressure (P), which is measurable in millimeters mercury/torr (mm Hg, torr), kilopascals (kPa), and atmospheres (atm),
Volume (V) is measurable in liters
Number of gaseous moles (n)
The temperature of the gas (T) is measurable in Kelvin (K)
The ideal constant is R, and it takes a variety of forms when different types of units are used. The three different formulations are as follows:
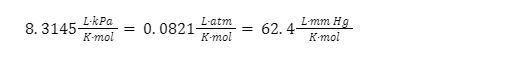
The ideal gases primarily opens up the possibility of examining the relationship between properties that are non-constant for ideal gases (n, P, V, T) for the time of three of these properties being fixed.
For the ideal gas equation scenario, the product of PV is proportional to T, which interprets that if gas has constant temperature, pressure and volume can increase until and unless the complementary variable decreases. This also interprets that if the temperature of the gas changes, it may be due in part to a variable change in volume or pressure. This equation is an integral tool as its approximation is good for low pressure and high-temperature gases.
Applying the Ideal Gas Law
The ideal gas equation allows the calculation of the value of the fourth variable for a sample of gas. If the values of three of the four variables (P, V, T, and n) are known. This also helps predict the final sample state of gas: its final temperature, pressure, volume, and amount, which follow other parameters such (As p, V, T, and n) specified at the early state. The most commonly used approach is to start with a very similar equation, i.e., the ideal gas equation, and the determination of the quantities is done after this same step for the necessary calculation.
CONCLUSION
The derivation of ideal gas law is from the empirical relationships of terms such as volume, pressure, temperature, and number of moles of gas. This can be used to calculate the properties if three are known or given.
Ideal gas equation: PV=nRT
