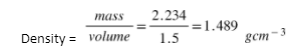Units and Measurements Solved examples

Physical quantities are used to measure standards everywhere. In every shop, you can get the units and measurements where anything you buy they measure it and according to their price they will sell the products. Now we are going to know more about them and solve problems we can face while measuring these amounts.

UNITS:

 A physical quantity’s unit is arbitrarily defined as a standard that is commonly accepted by society and may be used to measure other physical quantities of comparable nature.

MEASUREMENTS:

The measurement is a procedure that is essentially used in a comparison process. The magnitude of the number obtained is termed physical quantity and the standard is called Unit of a physical quantity.

STANDARD:

A standard of a physical quantity is the real physical indication of a physical quantity’s unit. For Example, The length of the side of a square is 4 cm. Here, 4 is the numeric value and cm is the unit.

Earlier there were three-unit systems used in different countries around the world. These systems were different from each other and led to difficulties. But now we use SI units of the system internationally. 

SOLVED EXAMPLES OF UNITS AND MEASUREMENTS.

Q1. Calculate the number of significant figures in 0.07500.

Sol: The number of significant numbers in a physical quantity’s measured value tells us how many digits we can trust. The greater the number of significant digits obtained in the measurement, the more accurate is the measurement. When counting the number of significant digits in a given measured quantity, the following rules are applied:

1. The non-zero digits are considered significant.
2. If a zero appears between two non-zero numbers, it becomes a significant figure.
3. Leading zeros, or zeros to the left of a number, have no significance.
4. The zeros to the right of the integer, or the trailing zeros, are significant.
5. The numerical part of exponential notation represents the number of significant numbers.

In the above figure 0.07500, 0.0 is non-significant, 7500 is significant. Hence, the number of significant figures in 0.07500 is 4.

Q2. Find the sum of numbers of 136.62, 223.5, 0.345.

Sol: The result of adding or subtracting two numbers with varying precisions should be reported to the same number of decimal places as the number with the smallest number of decimal places.

136.620

            + 223.700

            + 000.345

               360.665

Thus, the number can be rounded to 361.

Q3.  Find the density of a body in significant figures whose mass is 2.234 g and volume is 1.5 .

Sol: The answer to a multiplication or division problem is rounded to the same number of significant digits as the calculation’s least precise word. With the least significant figures, the result should preserve as many significant figures as the original number.

Thus, the number is rounded off and we get density = 1.5

Q4.   Two students were asked to note the mass of a body. Student A noted as 1.3 kg and Student B was noted as 1.32 kg. Which measurement is more accurate and why?

Sol: The measurement taken by Student B is more accurate. The measurement is taken up to two decimal points.

Q5. The density of a cube is determined by measuring one side’s length and mass. If the maximum error while measuring the mass is 2% and the volume is 4%. Calculate the maximum error possible while measuring the density?

Sol:  2 % + 3 * 4% = 14%.

Q5. In an experiment, a researcher takes 100 precise readings. If he does the same experiment again, this time taking 400 readings.  Calculate the factor by which the error will be reduced?

Sol: The probable error can be reduced by a factor of 4.

Q6. Calculate the number of significant figures in 0.05400.

Sol: The number of significant numbers in a physical quantity’s measured value tells us how many digits we can trust. The greater the number of significant digits obtained in the measurement, the more accurate is the measurement. When counting the number of significant digits in a given measured quantity, the following rules are applied:

1. The non-zero digits are considered significant.
2. If a zero appears between two non-zero numbers, it becomes a significant figure.
3. Leading zeros, or zeros to the left of a number, have no significance.
4. The zeros to the right of the integer, or the trailing zeros, are significant.
5. The numerical part of exponential notation represents the number of significant numbers.

In the above figure 0.05400, 0.0 is non-significant, 5400 is significant. Hence, the number of significant figures in 0.05400 is 4.

Q7. The density of a cube is determined by measuring one side’s length and mass. If the maximum error while measuring the mass is 3% and the volume is 5%. Calculate the maximum error possible while measuring the density?

Sol:  3% + 3 * 5% = 18%.

Conclusion:

Different things are measured in different parameters and different parameters are made by engineers to measure different things. This is how the system works and this should be maintained and used frequently to measure things. It helps a lot in day-to-day life to measure things in a while.