This article will go over some of the vector values used to characterize a body’s motion: position, displacement, velocity, and acceleration. These quantities are defined, and the mathematical relationships between them. For the scenario when the item travels in a straight line with constant acceleration, we develop certain functional connections between them and time (a scalar variable).
What is acceleration?
The rate of change of the velocity vector is defined as acceleration. The rate of acceleration might be constant or variable. In the event of constant acceleration, the ratio of net change of velocity to total time taken determines its value. Average acceleration is another name for it. Instantaneous acceleration is determined in circumstances when the acceleration changes with time.
A Uniformly accelerated motion
The uniformly accelerated motion is defined by a motion in a straight line with a constant acceleration and zero difference. Hence the velocity of an item in this movement continually changes depending on the velocity direction.
The main properties of uniformly accelerated motion: knowing the parameters of this motion is vital to determine whether we are talking about equally accelerated motion: Its motion in a straight line, indicating that it is only moving in one dimension. The fundamental difference between this motion and the constant velocity motion is that its acceleration is not zero. Its velocity is continually changing; due to acceleration, the velocity permanently grows or lowers; as a result, there will always be a beginning velocity and a final velocity in situations involving this motion.
The steady change in velocity is known as acceleration. If both acceleration and velocity have the same sign, the object will increase its velocity every second; however, if both magnitudes have different signs (for example, positive and negative acceleration), the object will begin to slow down every second until it reaches rest.
Some examples of Uniform Accelerated Motion are:
- A free-falling item.
- A frictionless slope with a ball sliding down it.
- Brakes applied to a bicycle.
A uniformly accelerated motion’s behavior
We usually take up and right directions as positives in a reference system and down and left directions as negatives, so if an object starts at rest and then receives a positive acceleration, the object will begin to move to the right. In contrast, if we apply a negative acceleration, the object will begin to move to the left.
When an object in uniformly accelerated motion has an acceleration in the opposite direction than the velocity, the object’s velocity will begin to decrease until it reaches rest; after a brief period of rest, the object will begin to advance in the opposite direction. An example of this is when we throw something up; we apply a velocity to the object, but gravity causes it to decrease its velocity; after a brief period of rest, the object will begin to advance in the opposite direction; after a brief period of rest, the object will
The Uniformly Accelerated Motion Formula in Physics
There are five formulas in physics for solving any uniformly accelerated motion problem, and we can use any of them to find a variable; however, we must know which one to use because some problems provide only specific data, but no data that can be used in an equation; therefore, we must choose carefully which equation we will use.
For example, if we wanted to calculate the ultimate velocity of an item and know the beginning velocity, acceleration, and distance, the first equation would not work since we would require the time. Instead, we would need to use the third equation because it has the same variables as we have.
Equations of uniformly accelerated motion
a = acceleration,
t = time the object has been accelerating,
vo = Initial velocity of the object,
vf = Final velocity of the object at time t,
∆x = displacement of the object during the time interval.
1st equation of motion: Vf = vo + at
2nd equation of motion: ∆x = vot + ½ at2
3rd equation of motion: ∆x = ½ (vf + vo)t
4th equation of motion: ∆x = vf t – ½at2
5th equation of motion: vf2 = vo2 + 2a∆x.
Conclusion
Acceleration may be uniform or non-uniform. The value and direction of a homogeneous acceleration are both constant. It’s critical to understand the equations of motion that explain an object’s motion under uniform acceleration. There are mainly two types of acceleration and this depends entirely upon the time in which the action is completed.
If the time period is constant then the acceleration is uniform and if the time period is variable or not taken into consideration then the acceleration is non-uniform and it is because of the time period only that the equations of these two concepts are different.

Instantaneous Acceleration
Instantaneous acceleration is the rate at which velocity changes using both speed and direction with respect to time such that the time interval goes to zero.
Formula:
The formula for instantaneous acceleration is :
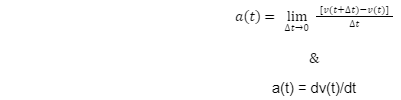
Derivation of the formula of Instantaneous acceleration
Instantaneous acceleration is the Average acceleration between two points that approaches a time limit of nearly zero. To find the formula for instantaneous acceleration we will go through the same basic formulas and from that, we will derive the instantaneous acceleration of any particle or anything moving particles.
Now we will use the general formula to determine the formula of instantaneous acceleration from the average acceleration with a time limit of nearly zero.
First, Expressing velocity (v) is a continuous function of time (t) and is denoted as v(t).
Now the average acceleration we know is ;
a = [v(t2) – v(t1)] / (t2-t1)
Now we need to find acceleration at any position so let, t1 = t and t2 = t+ ∆t and we know ∆t should be nearly zero so to calculate instantaneous acceleration putting ∆t nearly zero we will get
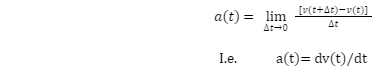
This is the required formula for instantaneous acceleration.
Some Solved Examples
Q1) The position of a particle is x(t) = 2t + 0.7t³ m. Find the instantaneous acceleration at t= 3 sec?
Ans: we have,
x(t) = 2t + 0.7t³
So,
v(t) = dx(t)/dt = 2+2.1t² m/s
Now,
a(t) = dv(t)/dt = 4.2t m/s²
Therefore,
At t = 3 sec instantaneous acceleration is;
4.2t = 4.2 × 3= 12.6 m/s² (Answer)
Q2) A particle is in motion and is accelerating. The position of the velocity is v(t) = 10t – 3t² m/s
- Find the functional form of acceleration.
- Find the instantaneous velocity at t= 1,3,4,5 s
- Find the instantaneous acceleration at t= 1,3,4,5s.
- Analyze the results of © in terms of acceleration and velocity vectors directions.
Ans: we have,
v(t) = 10t – 3t² m/s
- a(t) = dv(t)/dt = 10 – 6t m/s²
- v(1s) = 7 m/s
v(3s) = 3 m/s
v(4s) = -8 m/s
v(5s) = -25 m/s
- a(1s) = 4 m/s²
a(3s) = -8m/s²
a(4s) = -14m/s²
a(5s) = -20m/s²
At t = 1 sec, we have the velocity v(1sec) = 3 m/s which is positive; so both velocity and acceleration will be positive and in the same direction.
At t = 3 sec, we have the velocity v(3 sec) = 7m/s which is positive; so both velocity and acceleration will be positive and in the same direction.
At t = 4 sec, we have the velocity v(4sec) = -8m/s which is negative; so both velocity and acceleration will be negative and in the opposite direction.
At t = 5 sec, we have the velocity v(5sec) = -25m/s which is negative; so both velocity and acceleration will be negative and in the opposite direction.
(Answer)
Q3) The position of a particle is x(t) = 2t² + 0.7t m. What will be the instantaneous acceleration at t = 2 sec ?
Ans: we have,
x(t) = 2t² + 0.7t
So,
v(t) = dx(t)/dt = 4t+0.7m/s
Now,
a(t) = dv(t)/dt = 4t m/s²
Therefore,
At t = 2 sec instantaneous acceleration is;
4t = 4× 3= 12m/s² (Answer)
Conclusion
Instantaneous acceleration, average acceleration and formula for instantaneous acceleration plays an important role in day-to-day life. And it will help you to calculate acceleration at some instant which will help you to know how important this is and you will find applications of these things in different stages of life.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






