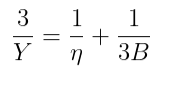Intermolecular forces in a solid
All matter, be it solid, liquid, or gas, is made up of atoms. Atoms join to form molecules. In a solid, the atoms and molecules are packed much closer together than in liquids or gases. Their arrangement is done in such a way that each molecule exerts a particular force on its neighbouring molecules. This force is known as the intermolecular forces in a solid.
The interatomic forces give structure to a molecule, whereas the intermolecular forces provide a structure to the material.
Elasticity
When an external force is applied to a solid body, it may get deformed or may get out of proportion. When a body is deformed, then internal forces develop inside that material to oppose the outside deforming force. The internal force tries to restore the body of the material to its original shape.
Thus, elasticity can be defined as the tendency of a body to retain its original shape after the deforming force is removed. The elasticity of every material differs. The more easily a body gains its original shape after the deforming force is removed, the more elastic that body is.
Perfectly elastic body
A perfectly elastic body is one that can regain its natural shape after the removal of the deforming forces. An example is quartz.
Partially elastic
Partially elastic bodies are those which only partially regain their original shape after the removal of the deforming forces. Neither are they fully elastic nor fully plastic.
Plasticity
A plastic body is one which stays in its deformed state even after the external force is removed. The original shape is unable to be restored even partially. This characteristic of a solid is called plasticity.
Stress
Stress can be defined as the ratio of the restorative internal force developed to oppose the deforming force to the area on which the force is applied.
In equilibrium, the magnitude of the stress produced is equal to the magnitude of the deforming force applied on a body.
Stress can be represented as:
Stress= ForceArea = FA
The SI unit of stress is given as N/m2
The unit of stress in CGS unit is Dyne cm-2
The dimensional formula is [M L-1 T-2].
Types of stress
Stress can be of two types:
Normal strain: Normal stress can be defined as the ratio of the restoring force to the area perpendicular to the surface of the body. It is then classified into compressive stress and tensile stress.
Tangential Stress: Tangential stress is when the restorative force is parallel to the surface area of the body.
Strain
Strain can be simply defined as the ratio of the change in shape or size of the body to the original shape or size of the body after the deforming force is applied. It does not have a unit.
Types of Strain
Strain is classified into three types:
Longitudinal strain: When the change in the shape of the body occurs along the length of the body, it is known as longitudinal strain. It is the ratio of the change in length of the body to the original length of the body.
Longitudinal Strain = change in length original length =
Volumetric strain: It is the ratio of change in volume of a body to the original volume. It can be represented as
Volumetric Strain =
Where V = original volume
= change in volume
Shear strain: Shear strain can be defined as the angular tilt in a body due to the tangential stress known as shear strain.
Now that we know what are the different forms of stress and strain, let us understand the relation between stress and strain.
Hooke’s Law
According to Hooke’s Law, a relation between stress and strain can be established. This law states that within the limits of elasticity, the ratio of stress to strain is a constant. This constant is known as Modulus of Elasticity. It can be represented as
Modulus of elasticity = StressStrain
As we know that strain does not have any SI unit, the modulus of elasticity takes the SI unit of stress. Thus, the SI unit of stress is given as N/m2
The unit in CGS unit is Dyne cm-2
The dimensional formula is [M L-1 T-2].
Young’s Modulus
Suppose we have a thin rod or wire which can increase in elongation according to the length. Then Young’s Modulus is defined as the ratio of longitudinal stress to longitudinal strain, given the elasticity limit is maintained.
Thus, Young’s Modulus can be represented as
Young’s modulus, Y = =
=
It has the same unit as that of the longitudinal stress as N/m2
It can also have its SI unit as Pa.
Bulk’s Modulus
It can be simply defined as the ratio of longitudinal stress to volumetric strain, within the limits of elasticity. It is represented as:
Bulk’s Modulus, K = =
Negative sign here represents that pressure variation and volume variation will always be negative to each other.
The opposite of bulk’s modulus is also known as compressibility.
Shear modulus or modulus of rigidity
Shear Modulus can be represented as the ratio of Tangential stress to shear strain.
Modulus of rigidity can be given as:
Modulus of rigidity η = Tangential StressShear Strain =
Poisson’s Ratio
Poisson’s Ratio is the ratio of lateral strain to longitudinal strain. Lateral strain can be defined as the ratio of change in diameter to original diameter, whereas longitudinal strain is the ratio of change in length to original length.
Poisson’s Ratio =
The value of Poisson’s ratio usually lies between 0.2 and 0.4 for most substances. Poisson’s ratio is maximum if a body is completely incompressible and the value is 0.5.
Now that we are aware of the different terminologies for the modulus of elasticity, let us understand the relations among Y, K, η and σ.
Relations among Y, K, η and σ
For isotropic materials, which means materials that have the same properties in all directions, two out of three elastic moduli are independent. Young’s Modulus could be expressed in terms of the Poisson’s ratio and Bulk’s modulus.
The relations among Y, K, η and σ can be expressed as
Also
Here Y = Young’s modulus
K = Bulk’s Modulus
η = Modulus of rigidity
= Poisson’s Ratio
Now, let’s see the process for relations among Y, K, η and σ derivation
Relations among Y, K, η and σ Derivation
Y = 3K (1 – 2μ)
Where Y = Young’s modulus
K = Bulk modulus
Conclusion
In this article, we learnt the different types of stress and strain that can affect a solid material. We also saw the relations among Y, K, η and σ, i.e., the different modulus of elasticity.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out