Profile
Settings
Refer your friends
Sign out
Kinematics- Laws Of Motion- Motion of a block on a horizontal smooth surface
The rate of change in the velocity of an object at any given time is defined as its acceleration. It is represented by “a”, and the units are m/sec2. Any item subjected to an imbalanced force, whether constant or variable, is said to be accelerated, as is any object that experiences a change in velocity, either in magnitude or direction or both. When a horizontal surface supports an object, the normal force is equal to the object’s weight. Additionally, basic friction is proportional to the normal force at all times. When an object is not on a horizontal plane, we must calculate the force perpendicular to the surface; this is a component of the weight.
An example is a body, with mass m, at rest on a horizontal table. The table’s normal response force (N) cancels out the gravitational force (mg). Assume a horizontal force F is applied to the body. We all know that a tiny amount of applied force isn’t always adequate to move the body. However, if the applied force F is the only external force acting on the body, it will have to move with an acceleration of F/m, regardless of how tiny. The body remains at rest because another force opposes the applied force F in the horizontal direction, resulting in zero net force on the body.
Let us go through the following cases for a better understanding of the motion of a block on a horizontal smooth surface:
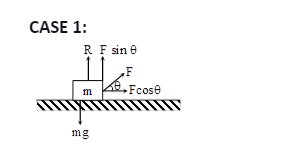
When a block of mass m is moved across a horizontal smooth surface at an angle:
The expression for reaction should be mg – F sinθ. When a block of mass m on a horizontal smooth surface is exposed to a pull acting at an angle to the horizontal, with no motion along the vertical direction.
It is assumed that the force acts at an angle of θ to the horizontal. As a result, we had to resolve the force.
The normal reaction (R) always operates upwards, while mg always acts downwards.
The forces acting in the upper and downward directions will nullify each other because there is no vertical movement.
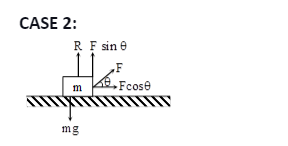
When a pull is acting at an angle (θ) to the horizontal (upward):
Now F has to be resolved into two components:
F cos θ along the horizontal and F sin θ along the vertical direction.
For zero motion in the vertical direction, we have R + F sin θ = mg or R = mg – F sin θ.
Hence, R = mg, R < mg.
For horizontal motion, F cos θ = ma
a = (F cos θ)/m
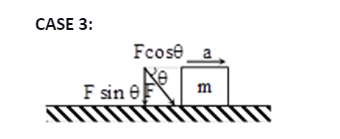
When a push is acting at an angle (θ) to the horizontal (downward):
The force equation in this case:
R = mg + F sin θ
For the horizontal motion:
F cos θ = ma
a = (F cos θ)/ m
Conclusion:
Observe the behaviour of a block of wood as it is slid across a flat, uncarpeted floor. As long as you provide a force on the block, it will continue to move. When the force ceases to exist, the block comes to a halt. After you stop applying force, the block will continue to slide for a bit. The force you’re exerting on the block isn’t the only one. A frictional force opposes the motion as well. Because of the frictional force, the block sliding over the floor comes to a halt. It would never cease if you could move the block across a surface with no friction.
