There are a few significant terms to be understood before mentioning the mathematical landscape of Ray Optics. The object position, represented by u, is the coordinate of the object with respect to the origin. As a convention, the origin in geometrical optics is taken as the Pole of the lens or the curved mirror involved. Similarly, the image position with respect to the origin is represented by the symbol, v. The heights of the object and the image are represented by the symbols ho and hi, respectively. Images that appear upright about the object are amalgamated in positive notes, whereas the inverted images are amalgamated with negative notes. Let us understand some basics of Ray optics before Magnification.
LIGHT REFLECTION IN SPHERICAL MIRRORS
The Laws of Reflection.
- I) The incidence angle (between the incident ray and the surface normal) and the reflection angle (between the reflected ray and the surface normal) are both equal.
- ii) At the point of incidence, the incident ray, reflected ray, and normal to the reflecting surface are all in the same plane.
The normal of a curved surface always passes through the centre of the curve. All distances are calculated from the mirror’s pole. The light incidence direction is usually taken as positive in sign convention. The distance measurement between two points in the opposite direction of incident light is taken as negative. However, the choice of the positive direction is arbitrary.
LIGHT REFRACTION
The Laws of Refraction:
- Snell’s Law: The sine of the angle of incidence and the sine of the angle of refraction have a constant ratio, called the refractive index between the media of transmission. In a mathematical form:
sin i
= constant
sin r
- The planes of the incidence ray, refracted ray and the normal to the point of incidence all lie on the same plane.
There is also a wave nature of light that is at play. According to wave nature, light experiences phenomena such as interference and diffraction. In general, light is electromagnetic energy that generates the sensation of vision. Let us explore how the wave nature light is idealised as the ray optics in specific situations.
– The wavelength of visible light ranges from 400 to 750 nanometers.
– Light travels at the quickest speed conceivable in nature in a vacuum, which is 3.0 x 108 m/s
– Because light waves have such a small wavelength in comparison to the size of regular things, they are thought to move in a straight path between two sites.
– A beam of light, on the other hand, is an idealisation of the wavefront. It’s a light route that runs in a straight line between two places. A light beam is made up of a collection of rays.
– Reflection, refraction, interference, and diffraction are examples of optical phenomena.
What is Magnification?
We can accurately describe the location and size of an image by using the rules of ray tracing and making a scale drawing with paper and pencil. However, the real advantage of ray tracing is that it allows you to see how images are formed in a variety of situations. We use a pair of equations derived from a geometric analysis of ray tracing for thin mirrors to obtain numerical data. The mirror formula is as follows:
Mirror equation
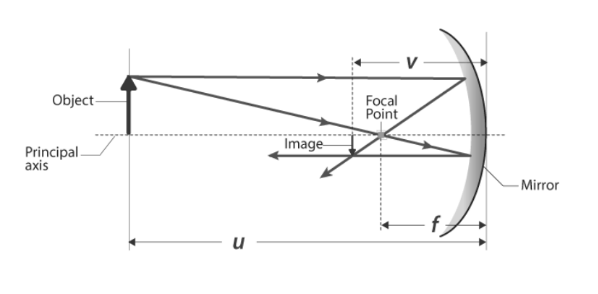
Ray tracing should be done by following the following steps:
- A ray passing through the focal point of a converging lens exits parallel to its axis.
- A ray that enters a diverging lens and travels to the opposite side’s focal point exits parallel to the axis.
- What is the procedure for creating a picture of an item using a lens? The ray-tracing technique may be used to explain how lenses produce pictures. We may also use equations to quantitatively explain the visuals. The following are the five essential ray tracing rules to remember:
- A beam entering a converging lens parallel to its axis, on the other hand, goes via the focal point F of the lens. The ray’s source seems to enter a diverging lens parallel to its axis at focal point F.
- A light travelling through the centre of a converging or diverging lens maintains its orientation.
Consider the case of an item that is far away from the convex lens, as shown in figure 2. We follow the trajectories of chosen incoming light originating from one place on the surface (in this example, the top of the person’s head) to establish the position and size of the picture generated. Rays can move in many directions from this point, but we’ll focus on a few that have well-defined paths:
2nd diagram
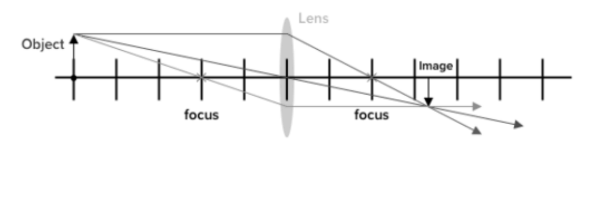
- The first ray must enter the lens parallel towards its axis and exit through the focal point on the opposite side.
- The second ray does not change direction as it passes through the centre of the lens.
- On its way into the lens, the third ray passes via the closer focal point and exits parallel to the axis.
- On the other side of the lens, the three rays cross at the same point. It is where the image of the top of the person’s head is located.
- All rays that originate from the same juncture on the person’s head are reflected so that they cross at the point depicted.
- Rays from another point on the surface, such as her belt buckle, would then intersect and form a complete image, as shown.
- Even though three rays are traced, only two are required to find the image. It is preferable to trace rays for which simple ray tracing rules exist.
Calculation of Magnification:
The magnification m is defined as the ratio of image height to object height ho and hi. The following relationship exists between magnification and the positions of the image and object:
m = hi/ho = -v/u
And the similar formula for a lens is given by:
m = hi /ho= v/u
These equations can be used to find out the magnification of the object without having data about its height.
Conclusion
Lenses may be found in a wide range of optical equipment, from a simple magnifier to a camera lens to the lens of a human eye. The term “lens” is derived from the Latin word “lentil,” which has a convex lens-like form. All light rays entering the convex lens with comparison to its axis intersect at a certain point on the opposite side. The principal axis is a line that passes through the lens’s centre and is perpendicular to it. The light rays coming parallel to the principal axis will either converge or diverge on a point on the principal axis called the focus. A collection of rays passing through the lens shows how the beam changes direction as it enters and exits the lens.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






