Profile
Settings
Refer your friends
Sign out
Acceleration: The rate at which velocity changes is called acceleration, and it is a function of time. Therefore, the second derivative of position as a function of time can be used to evaluate the acceleration. This quantity is a vector quantity because it is associated with both magnitude and direction. This quantity is denoted by “a.” In physics, acceleration is measured in metres per second squared, or in metres per second (the object’s speed) per second, or in m/s2 (metres per second). Acceleration can be negative, zero, or positive. Positive acceleration occurs when the velocity of an object increases with time. A zero velocity is called a zero acceleration, whereas a negative acceleration, also known as a retardation, indicates a decreasing velocity over time.
Types of Acceleration
Average Acceleration
It is said that an object is accelerating when its velocity changes. The average acceleration, a¯ , is the change in velocity per unit time, or the rate of change in velocity. The acceleration units are distance over time squared. Symbols with a bar over them have the meaning “average”; so “a-bars” stand for average acceleration.
Formula: av = Δ v / Δ t
For Example: In 5.00 seconds, a car accelerates from rest to a speed of +60.0 km/h on a straight road. Approximately how fast does the car accelerate on average?
Ans. The acceleration is expressed in kilometres per hour per second in this problem. Unit expressions should not contain two different units for the same quantity. Having both hours and seconds is not desirable in this case. Hence, the hour units are converted to seconds. By converting 60.0 km/h to m/s, we get 17.0 m/s.
17.0 m/s divided by 5.00 s = 3.40 m/s2
Hence, The acceleration is 3.40 m/s2.
Instantaneous Acceleration
Acceleration that occurs at some discrete instant in time is called instantaneous acceleration and can be determined by taking a derivative of the velocity function. Simply put, instantaneous acceleration is the rate at which velocity changes in relation to time. To calculate acceleration, we need to take the limit of the rate of change of velocity with respect to time, since the change in time approaches zero. For calculating instantaneous acceleration, calculate the average velocity between two points in space separated by Δt and let Δt approach zero. Based on the derivative of the velocity function v(t), which represents the instantaneous acceleration, the result is obtained.
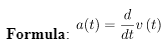
For Example: Given the particle’s position x(t) =3.0t + 0.5t3 m. Calculate the particle’s instantaneous acceleration at t = 2.0 s.
Ans. Here, x(t) = 3.0t + 0.5t3 m
So, v(t) = dx(t)/dt = 3.0 + 1.5t2 m/s .
Therefore, a(t) = dv(t)/dt = 3 t m/s2………..(a)
Hence, at t = 2 seconds, instantaneous acceleration of the particle is 3t = 3.2 m/s^2 = 6 m/s^2
Acceleration Due to Gravity
An acceleration due to the gravity of the earth is an acceleration resulting from gravity. As a result of the earth’s gravitational pull, all objects fall towards the earth. Moreover, when bodies fall freely, they have some velocity, so they will experience some acceleration as well. The acceleration that occurs due to gravity is known as gravitational acceleration. Gravitational acceleration is a vector quantity. It is expressed as g. The value of g is 9.8m/s2. Since earth isn’t a perfect sphere, the value of gravity varies from place to place on its surface. There is a difference in the radius of earth near the equator and at the poles. In such a case, gravity’s standardised value (g=9.8 m/s2) changes. As a consequence, gravity’s acceleration increases gradually from the equator to the poles. In all cases, objects in free fall under the influence of gravity at the same point on Earth experience the same acceleration, g, regardless of their mass.
Conclusion
A vector quantity such as acceleration measures the rate at which the velocity of an object changes, and the three ways in which the velocity of an object may change are its direction, speed, or both direction and speed. Due to gravity’s parallel and perpendicular components, the tennis ball’s speed increased as it moved down the plane. These components cannot be observed when the ball is rolling on a flat surface. An inclination increases the speed of the ball and changes its direction from upward to downward. Due to the inclination’s ability to increase the ball’s velocity, a ball will accelerate down an inclined plane. Travel distance increases with time squared. You can determine the acceleration by subtracting the initial velocity from the final velocity and dividing that result by the time.
