A mean free path is used, especially when it is difficult to measure random motion. This concept can be understood by looking into the molecular nature of matter. The molecules in solids are packed compactly with no space, while those in liquids are relatively less compact. In gases, the molecules are loosely packed and have a lot of intermolecular spaces. When these are not subject to inter-particle interactions, it is known as an ideal gas. Therefore, the definition for the mean free path would be nothing but the distance between 2 consecutive collisions. The symbol λ is used to represent the average distance covered by a particle in between collisions with other particles. The distance between collisions is the free path denoted by λ1, λ2, λ3, etc.
What is the Mean Free Path?
The theory of mean free path is considered a kinetic theory. It is used primarily to interpret and explain the structure and composition of molecules concerning sub-microscopic particles. Mean free path, according to science, is defined to be the path or the average length on which the travelling particle due to one and/or more number of successive collisions along with several particles changes its course, direction or energy. In some specific cases, this change may occur even in the form of changes in the properties of the particles.
Mean Free Path’s Derivation
Mean free path formula is mathematically expressed by using the following formula –
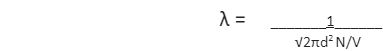
The derivation of the mean free path formula is based on certain assumptions. Firstly, the molecule or particle considered is a sphere. Secondly, the molecule in question is moving and colliding with other particles and the walls of the container, whereas the rest are stationary. The area of cross-section of the sphere here is πd2 and the volume of the cylinder is πd2 × vt, where v represents the velocity of the molecule and t represents the time. The number of molecules per unit volume can be written as N/V. The mean free path is expressed as –
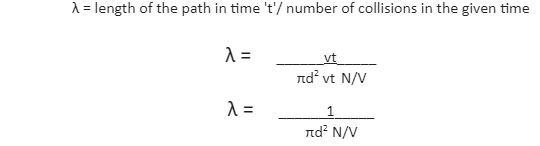
The derivation of the mean free path formula is based on certain assumptions. Firstly, the molecule or particle considered is a sphere. Secondly, the molecule in question is moving and colliding with other particles and the walls of the container, whereas the rest are stationary. The area of cross-section of the sphere here is πd2 and the volume of the cylinder is πd2 × vt, where v represents the velocity of the molecule and t represents the time. The number of molecules per unit volume can be written as N/V. The mean free path is expressed as –
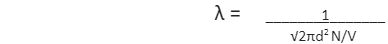
Scattering Theory
If a beam of particles is shot through a target that is in the form of a thin slab, some of the beam particles are stopped by the slab. If it is assumed that the beam particles are the only particles in motion and the rest of the particles are stationary or at rest, we can arrive at a formula to determine a mean free path. The formula is represented as follows –
l = (no)-1
In this formula, l represents a mean free path, n is the number of target particles or molecules per unit volume, and o is the effective cross-sectional area for collision. The probability of a beam particle or molecule stopping in that slab is the net area of the stopping atoms divided by the total area of the slab. σ is also known as the scattering cross-section. The particle’s fraction of molecules that do not get blocked by the present slab is the transmission.
Gases’ Kinetic Theory
Kinetic theory of the gases is described as the average length the particle or molecule travels in-between a collision relative to many other particles. The formula for the scattering theory was based on the assumption that the molecules or particles are at rest. Thus, in a real case, the beam particle moving with a very high-speed v having the velocities of similar particles present in random locations or motions applies to the formula l = (no)-1. In the case of gaseous molecules, the movements of the target molecules are comparatively insignificant, making the (v) relative velocity approximately equal to the average velocity and the (s) relative speed becomes √2v. This indicates that clashes are √2 times the numeral with any stationary target particles. The number of collisions is √2 times the number with stationary targets. In a given practice, the diameter of gases molecules is not properly defined and kinetic diameter is defined in terms of the mean free path. Gas molecules are different from solid molecules.
Conclusion
Mean free path theory is used to analyse and estimate the average distance the molecules have between one or more collisions. This theory becomes very important in gaseous substances as the molecules are loosely packed with a lot of intermolecular space compared to solids and liquids. It becomes difficult to understand the distance or path the particles follow when they collide with either each of them or with the walls of the containers they are restricted to. This is when a mean free path theory becomes important to analyse and solve these challenges.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






