Profile
Settings
Refer your friends
Sign out
Properties of gases are easier to understand than those of solids and liquids. This is mainly because, in a gas, molecules are far from each other, and their mutual interactions are negligible except when two molecules collide.
An ideal gas is made of the molecules on which no external forces are acting except the forces formed upon collision with one another and with the wall of the container in which they are packed. Conditions for ideal gas are :-
- Incessant movement
- Very little volume and intermolecular forces.
- Perfectly elastic collision between molecules.
- Kinetic energy should be proportional to the ideal gas’s absolute temperature.
Definition of the Ideal gas equation
Ideal gas equation is the mathematical equation of the state of hypothetical gases, which are assumed to be ideal. It combines empirical laws such as Charle’s law, Boyle’s law, Gay-Lussac’s law, and Avogadro’s law. This equation can be derived using the kinetic gas equation.
Derivation of Ideal Gas Equation from Kinetic Gas Equation
According to the kinetic gas equation,
PV= ½ mnu2
Where P is pressure,
V is volume,
m is the mass of one molecule,
n is the number of molecules,
u is RMS velocity.
Definition of terms used in Ideal gas Equation
P= Pressure = Perpendicular force exerted per unit area by the gas molecules.
V= Volume= Space occupied by the molecules in a container.
n= Number of moles= Amount of gas measured in terms of moles.
R=Ideal gas Constant= It is the product of pressure and volume of one gram molecule of ideal gas divided by the absolute temperature.
T= Temperature= Measured as the degree of hotness of the body.
Forms of Ideal Gas Equation
1. Common form.
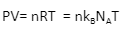
Where,
P = pressure of the gas.
V= volume of the gas.
4. Combined gas law
A combination of the laws of Charles, Boyle, and Gay-Lussac gives the combined gas law. It takes the same functional form as that of the ideal gas law, and in this law, the PV to T ratio is taken as constant k. The number of moles is unspecified.
Thus the equation becomes,
PV/T = k
Where P is the pressure, T is absolute temperature, V is volume, and k is a constant.
If you compare the same substance in different conditions, the law becomes,
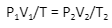
Conclusion
Thus, we can conclude that the ideal gas equation is applicable only for the ideal gases and not for all the gases. It can’t be applicable for the gases which have remarkable volume, high intermolecular forces, have inelastic collision, and do not have the kinetic energy proportional to the absolute temperature of the ideal gas. Thus, the Ideal gas equation has limitations. It doesn’t work at the conditions when the temperature is low, density is high, and the pressure is extremely high because at this condition, the molecular mass and the intermolecular forces matter. It cannot be applied to heavy gases like refrigerants and gases with very high intermolecular forces like water vapour.
