Gravitation-Variations in Gravitational Potential
Every object possesses some energy in a position (i.e., in a gravitational field or electric field) or in a stretched or compressed situation that is called its potential energy. The amount of work done to bring a unit mass to the gravitational influence of the source mass from infinity is called Gravitational Potential. It is represented by the symbol “V”. Its SI unit is J/kg.
Characteristics of Gravitational Potential
- When an object approaches an attractive body, it travels from higher to lower potential and hence the Gravitational Potential always results in a negative value.
- Gravitational potential is not affected by the direction of motion and therefore is a scalar quantity.
- At a distance of infinity from the attracting body, Gravitational potential is maximum, and its value is zero.
- Its dimensions are [ M0L2T-2].
- The CGS unit of gravitational potential is erg g-1.
- If the gravitational potential is equal on all points, the surface is called an equipotential surface.
Similarities and Difference Between Gravitational and Electrostatic Potential
- The law of gravitation and Coulomb’s law or the law of electrostatic repulsion both are derived from the same quantitative relationship between mass and distance. Therefore, the study of gravitational potential shares a lot of similarities with the study of electrostatic potential.
- The first similarity between the gravitational and electrostatic potential is that the forces that give rise to them depend inversely on the distance between two non-zero mass bodies in an ideal environment. In the case of gravitational potential, one of the objects is fixed like the earth. The second object can be a body in the gravitational field of the earth.
According to the law, if the distance between the earth and the body is r, the gravitational force responsible for the gravitational potential is inversely proportional to r2. Similarly, in cases of electrostatic potential, the electrostatic force responsible for it is inversely proportional to r2 ,if r is the distance between these forces.
- The second similarity is that these quantities are defined as the work that has to be done. When a gravitational potential is determined at any point A, it is defined as the work that has to be done against the gravitational force in moving a body to A from an arbitrary point, usually infinity.
The same statement can be tweaked to fit electrostatic potential. It can be defined as the work that has to be done in moving a charged body to point A from an arbitrary point, usually infinity. Thus, both the properties are only valuable when some distance has to be put between the two objects that are the experiment’s subjects.
- However, one major difference between gravitational and electrostatic potential is the type of force involved. Electrostatic potential arises from the electrostatic force. The electrostatic force has two types – It can be an attracting force or a repulsive force. The polarity of the charge decides this.
But gravitational potential arises from gravitational forces. Gravitational forces exist between two bodies by virtue of their masses and, therefore, are always attractive in nature.
Expression of Gravitational Potential
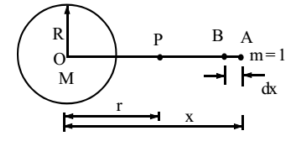
R= Radius of earth
M= Mass of earth
P= Point at the distance r
A = Point at the distance of x from the centre of the earth
O= Centre of the earth
M = Unit mass at A
Force acting on unit mass at A
F = GMmx2=GM(1)x2=GMx2
If the mass moves a short distance dx from A to B, then the work done will be :
dW=F.dx=GMx2dx
Total work done by integrating the above equation :
W=rGMx2dx=GMr1x2dx
W=GMrx-2dx=GMx-1-1r
W=-GM1xr=-GM1r–1
W=-GM1r-0
W=-GMr
This work, Gravitational Potential, at the point given by the equation:
V=-GMr
G= Gravitational Constant
M= Mass of the earth
Gravitational Point Due to Earth or Solid Sphere on Different Point
- Outside earth ( r > R)
– GM/r
Here the distance between the two bodies is greater than the radius of curvature of the earth denoted by R.
- On the Surface (r=R)
– GM/R
Since the object is at the surface of the earth, the distance between the centre of the earth and the object is equal to the earth’s radius.
- Inside the earth surface (r < R)
-GM[ 3R²-r²/2R³]
Inside the earth’s surface, the distance between the object and the earth becomes lower than the radius of the earth. Also, a reduced mass of the earth is acting upon the object since it is inside the earth.
- At the centre (r =0)
-3/2[GM/R]
Gravitational Potential Hollow Sphere at different points
- Outside the shell (r > R)
– GM/r
- On the surface (r = R)
-GM/R
- Inside the shell (r < R)
-GM/R
Conclusion
At any point in a gravitational field, the gravitational potential can be calculated as the work that has to be done to accomplish the task of bringing a large object from some defined position (that has zero potential like infinity) to that point. The gravitational field has to do work in bringing a mass from infinity to the earth’s surface, and therefore the gravitational potential energy at the earth’s surface is negative. If a body is to be removed from the earth’s gravitational field, work has to be done against gravity.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out