All around us objects undergo acceleration. The motion of planets around the sun, vehicles accelerating on the highways, objects in freefall etc. Acceleration describes the motion of objects, that is, whether the velocity is increasing or decreasing or whether it’s just remaining uniform. Hence, it is essential to understand motion before attempting to understand acceleration.
Motion
Motion is a state where an object changes its position with respect to a point that has been considered stationary by the observer or with respect to the observer himself. Motion is relative, that is, an object which appears stationary to someone might actually appear in motion to another observer. This point of view is called the frame of reference. For example, for an astronaut stationed at the International Space Station, earthly monuments like the Taj Mahal might appear moving, but to someone standing and admiring their beauty on Earth’s surface, they will remain at rest. Let’s take another example. The Sun appears moving to us, but we know that the Earth itself is moving.
There are various types of motion, such as rectilinear (straight line) motion, circular motion etc. They are also classified on the basis of their velocity, whether it’s changing or not, as uniform and non-uniform motion. For objects in rectilinear motion with uniform velocity, the components of motion (velocity, acceleration and distance) can be predicted by the use of certain equations. These equations were discovered by the famous scientist Galileo Galilei and are called the equations of motion or the equation of kinematics.
Equations of Motion
- v=u+at
v= final velocity of the object
u=initial velocity of the object
a=acceleration of the object
t=time taken for motion
- s=ut+1/2at2
s=distance covered by the object
u=initial velocity of the object
t=time duration of motion
a=acceleration of the object
- v2-u2=2as
v=final velocity of the object
u=initial velocity of the object
a=acceleration of the object
s=distance covered
Derivation of the Equations of Motion
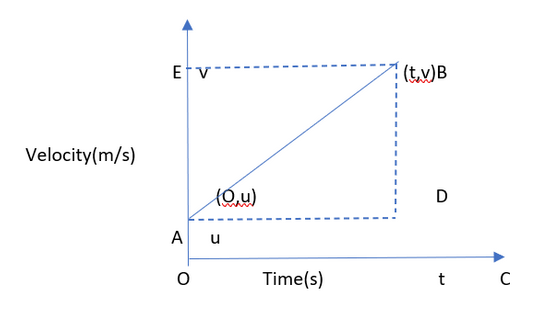
- Let us consider a velocity-time graph for a body.
The body has initial velocity u (measured by line OA). The object is uniformly accelerated motion (the slope is a straight line inclined to the X-axis). The acceleration value is a. The object reaches its final velocity v (measured by line OE). The time duration of this motion is t seconds. Let the distance travelled covered by the object in time t be s.
u=OA, v=BC, t=OC
The slope of the velocity-time graph=acceleration of the moving object
a=(yb-ya)/(xb-xa)
a=(v-u)/(t-0)
at=v-u
On rearranging,
v-u=at OR
v=u+at (first equation of motion)
- Distance covered by the object is equal to the area under the graph for the velocity-time graph.
s=area of OABC
=area of rectangle OADC+area of triangle ABD
=(length*breadth)+½*base*height
+OA*OC+½ *AD*BD _______________(1)
From the graph, we know:
AD=OC=t
BD=EA=OE=OA=v-u
Substituting in equation (1):
s=(u*t)+½ *t*(v-u)
Using at=v-u:
s=ut+½ *t*at OR
s=ut+½ at2 (Second equation of motion)
- Distance travelled=area of trapezium OABC
s=½*(sum of parallel sides)*height
=½(OA+BC)*OC
=½(u+v)*t
Using t=(v-u)/a:
s=½(u+v)*(v-u)/a
=½(v+u)(v-u)
2as =(v2-u2)
v2-u2=2as (Third equation of motion)
The equations of motion are only applicable, however, in cases, where:
- Motion is rectilinear.
- Acceleration is uniform.
Types of Motion
Motion can be of numerous types. It is not that everything moves in the same fashion. For instance, it can be in a straight line, or in a circle. Therefore, the motion has been classified into several different types. The most basic classification of motion consists of four main types of motion. These are:
- Rotary Motion- In this type of motion, the object revolves around a circular path continuously. For example, the motion of the hands of the clock, the motion of the blades of a ceiling fan etc.
- Oscillatory Motion- In this type of motion, the object follows a to and fro path continuously for the time duration of motion. For example, the motion of a simple pendulum, the movement of a spring etc.
- Linear Motion- The motion of an object in a straight (linear) path is referred to as rectilinear or linear motion. Examples of this type of motion include the motion of an athlete on a straight racing track, the motion of light rays etc.
- Reciprocating Motion- In this type of motion, the body continuously moves backwards and forwards. The main difference between oscillatory and reciprocating motion is that in oscillatory motion, the object moves to and fro, while in reciprocating motion, the object moves backwards and forwards. Examples of reciprocating motion include the motion of needles in a sewing machine, the motion of a doorbell ringer etc.
Examples of Accelerated Motion
The following are some examples of motion involving acceleration (positive or negative):
- The freefall of objects.
- The circular motion of objects.
- The motion of vehicles on the road.
- A ball launched up in the air
Conclusion
An object is said to be in accelerated motion if its velocity changes throughout the course of its motion. It is the rate of change of motion per unit time. Acceleration can be either positive or negative. If the acceleration is negative, the motion is also known as retarded motion. In cases pertaining to rectilinear motion with uniform acceleration, the components of motion can be predicted by using the equations of motion. There are three equations of motion. The slope of the velocity-time graph gives acceleration while the area under the velocity-time graph represents the total distance.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






