Projectile motion is a type of motion that an item or component (a projectile) experiences when it is thrown near the Earth and travels along a bent route only due to the gravitational force. Galileo demonstrated that this curved route is a parabolic curve or a parabola, although it might also become a straight line in a particular situation once it is hurled directly skyward. Ballistics is indeed the science of all such actions and motions and such a trajectory is termed a ballistic trajectory. It can also be said as the path of a projectile.
So, we saw that the path of a projectile is mostly parabolic. But, it doesn’t mean that the equation of the trajectory will be y2=4ax or y2=-4ax. Whereas, it’s quite complex which we’ll see along
So, what can be the equation of the trajectory or the path of the projectile when thrown elevated, it is

Where,
y = vertical component
x = horizontal component
g = acceleration due to gravity
= angle from which projectile is thrown
v = absolute initial velocity
Now, similar to this there are many other formulas also which define the property of the trajectory or the path of the projectile motion. Usually, if we divide it into vector parts, similar to any other elevated vector it also produces a vertical and horizontal vector as shown below.
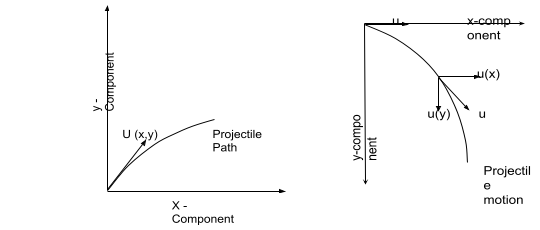
The x-component determines the horizontal velocity and other parameters of the projectile, whereas the y component determines the vertical velocity and other parameters of the projectile. Where on the right the horizontal projectile motion is shown with its vectors.
The important properties of a projectile that comes under the topic of the equation of path of a projectile are the initial velocity, projectile’s time of flight, acceleration, velocity and displacement, the parabolic trajectory equation (already written above), the maximum height and the range of the projectile. Most of these include both the vertical as well as the horizontal projectile motion data. Let us see them one by one also describing their motion in their planes formulas,
In the below formulas the terms used are as,
ux = initial velocity in x direction/component
uy = initial velocity in y direction/component
= Angle of elevation during throw of the projectile
g = acceleration due to gravity
ax and ay = acceleration in x and y direction/component respectively
x and y = coordinate positions or positions in space in x and y direction/component respectively
t = time
Initial velocity
Initial velocity is obtained during the launch of the projectile, which is usually shown as the components of x and y coordinates as,
ux=ucos
uy=usin
Acceleration, velocity and displacement
Speaking of acceleration, for a projectile motion there happens no acceleration in the horizontal plane whereas it happens in the vertical place as free fall due to gravity. The equations are as,
ax=0
ay=-g
The acceleration remains the same for horizontal projectile motion
In the case of velocity, the horizontal velocity stays the same, whereas vertical velocity changes in a linear manner. The equations are as,
ux=ucos
uy=usin-gt
and in horizontal projectile motion it is as,

And for the displacement, one can find the same (x and y coordinates) at time t, using formulas,
x=utcos
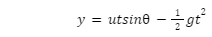
Time of flight projectile formula
The time of flight depicts the time required or the time the projectile will take to reach its destination. It can be expressed as,

These are also said as the total flight time.
Maximum height of the projectile
Coming to the maximum height an object can reach can be given as,

Where the projectile’s motion horizontal component does not come as this parameter solely depends on vertical displacements of the projectile.
Maximum Range of the projectile
The maximum range tells us how far in the horizontal distance an object can go having its prerequisites. Opposite to maximum height, this parameter contains projectile motion’s horizontal component and the equation for the same in elevated projectile motion is given as,

Conclusion
To sum up, the motion of a projectile is mostly parabolic, whether it is the example of throwing a ball or spraying water in any direction except vertically upward or downward direction. But instead of a simple parabolic equation the equation for elevated motion is written

Similar to the trajectory equation there are some other parameters and their equation that determines important objectives of the trajectory. They are different from each other in both the conditions, in elevated projectile motion and horizontal projectile motion
Some of the important parameters and formulas are the range of the projectile formula, maximum height formula, acceleration, velocity and displacement formula, time of flight formula and the initial velocity formula.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






