Profile
Settings
Refer your friends
Sign out
Both in rotational and translational motion a hard body can move, both the angular and linear velocities can be examined under such circumstances. It is very much required to individually define the motions of rotational nature and translational motions of a body to make it easier to understand. Given below are some quantities that are related to linear motion and their analogues in rotational motion.
Linear Motion | Rotational Motion about a Fixed Axis |
Work dW = F ds | Work W = dθ |
Acceleration a = dv/dt | Angular acceleration a = d/dt |
Kinetic energy K = Mv2/2 | Kinetic energy K = I2/2 |
Displacement x | Angular displacement |
Power P = Fv | Power P = τω |
Force F = Ma | Torque =Ia |
Mass M | Moment of inertia I |
Velocity v = dx/dt | Angular acceleration a = d/dt |
Linear Momentum p = Mv | Angular momentum L = I |
Rotational Motion
Rotational motion is defined as in the space around a fixed point the motion of an object in a circular path. With a common angular velocity when all particles of a body move in circles around an axis, the motion of the particular body that does not change shape or deform is called rotational motion. For example – The Earth’s motion; all the particles of the Earth move in circles around an axis with a common angular velocity, but the body that is in motion (here the Earth) does not change its shape or deform. The same condition occurs with the motion of a wheel, motors, etc. in a vehicle. As force and mass play the role in linear motion, in the same way torque and moment of inertia play a similar role in rotational motion.
Rotational motion about a fixed axis
Due to the fixed axis, components that are in a similar way of the fixed axis only the torque are considered. These are the only components that can rotate the body around its axis. A composition of the torque from its current position will tend to turn the axis away that is perpendicular to the rotational axis. By allowing the axis to be in a fixed position, it can be predicted that proper constraint forces will happen to cancel or the influence of the perpendicular components of the torques will cancel. As a result of these, there is no requirement to consider the perpendicular components of the torques. It explains that on a rigid body for calculating torques
- The thing that is required to be considered is only the forces that are perpendicular to the axis and are present in planes. The thing that is not required to be considered is the forces that are parallel to the axis which gives rise to torque that is perpendicular to the axis.
- The component that is only required to be considered is the place of the vectors which are at right angles to the axis. The component that is not required to be considered is the position vector component which is in alignment with the axis which will in turn result in torques at right angles to the axis.
Inertia meaning
The meaning of inertia in Physics is the inability of an object to change its state of rest or motion in a particular direction. Simply, inertia can be explained as when an object is in rest tends to remain in rest but when the object is in motion tends to remain in motion.
Moment of inertia meaning
The measurement of an object’s adverse to rotational change is the moment of inertia. The moment of inertia is measured in kilograms per square metre (kgm2) and is represented by ‘I’.
Moment of inertia is expressed as I = Mr²
Here,
M = Mass of the particle
r = Distance from the rotation axis
Following are some of the symmetric bodies with symmetric axis Moment of inertia –
The relationship between torque, a moment of inertia, and angular acceleration is
net =Ia
or
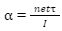
Here, net = Total torque from all forces relative to a chosen axis.
Conclusion
It is to conclude that rotational motion is defined as in the space around a fixed point the motion of an object in a circular path. Due to the fixed axis, components that are in a similar direction of the fixed axis only the torque are considered. These are the only components that can rotate the body around its axis.
