Profile
Settings
Refer your friends
Sign out
In day-to-day life we use motorcycles, vehicles but we can’t calculate the speed by viewing a vehicle because we don’t know how to calculate. For application you need to learn from methods, formulas. Speed and velocity are located everywhere and to calculate these we use average velocity, instant velocity and to calculate speed we use average speed and instant speed. Let’s learn more!
Instantaneous velocity
The rate of change of position in a particular direction concerning small or negligible time intervals is known as Instantaneous velocity. It gives the value of an object in motion at a specific time.
Unit: The unit for instantaneous velocity is m/s.
Quantity: Vector
Formula:
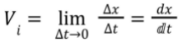
Example: Find the instantaneous velocity of an object travelling south and covering 80m in0. 4 sec. What will be the instantaneous velocity?
Answer: The instantaneous velocity of the object travelling south and covers 80m in 0.4 sec is
Instantaneous velocity = distance/ time = 80/0.4 = 200m/s.
Hence the object travels at an instantaneous velocity of 200m/s towards the south.
Average Velocity
Average velocity is the ratio of total displacement over time. Instantaneous velocity can be said as average velocity when we restrict the time period to zero.
Formula explanation:
As we discussed instantaneous velocity is the rate of change of velocity in a small period of time in a particular direction. Now to illustrate the formula first,
Let x is the continuous function of t and is denoted by x(t). As we know for instantaneous velocity the limit ∆t tends to 0. We have the formula to find the average velocity between two points is;
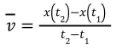
Now to find the instantaneous velocity;
Let t1 = t and t2= t+ ∆t. And put the limit ∆t tends to 0.
Putting these values we will get
The instantaneous velocity of an object is the derivative of x with respect to t. I.e
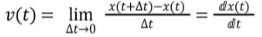
Instantaneous Speed
The rate of change of position concerning small or negligible time intervals is known as Instantaneous speed.
Instantaneous Speed formula:
Example: If a bike covers 8m in 0.4s then what will be the instantaneous Speed?
Ans: Instantaneous Speed = distance/time = 8/0.4 = 20m/s
Average speed
It can be defined as the average rate of change in position with respect to total time.
Average speed Formula: Average speed = total distance travelled ÷ total time
Unit: m/s or km/h
Difference between speed and velocity
The difference between speed and velocity is Speed is the change of position with respect to time but Velocity is the change of position with respect to time in a particular direction.
An Example of speed: A bike is riding at a speed of 60kmph.
An Example of velocity: A bike is riding at a speed of 60kmph towards the north.
Some solved examples of Instantaneous Velocity:
- Find the Instantaneous velocity of an object travelling along a straight line for 5 sec time with a position function x defined as 5t²+2t+4?
Answer: The given function is
x = 5t²+2t+4
Differentiating the given function with respect to t, we will get
Substituting ‘x’ value we will get,
Thus the instantaneous velocity for the above function is 52m/s.
- Find the Instantaneous velocity of an object travelling along a straight line for 3 sec time with a position function x defined as 2t²+4?
Answer: The given function is
x = 2t²+4
Differentiating the given function with respect to t, we will get
dx/dt = 4t
Now we have t=3s, putting t=3s we will get the instantaneous value as,
dx/dt = 4t+2 = 4×3+2= 14m/s
Thus the instantaneous velocity for the above function is 14m/s.
- Find the Instantaneous velocity of an object travelling along a straight line for 1sec time with a position function x defined as (⅔)t²+4?
Answer: The given function is
x =( ⅔)t²+4
Differentiating the given function with respect to t, we will get
dx/dt=2×( ⅔)t=( 4/3)t
Now we have t=5s, putting t=5s we will get the instantaneous value as,
dx/dt= (4/3)×5=20/3 = 6.67m/s
Thus the instantaneous velocity for the above function is 6.67m/s.
Conclusion
Instantaneous speed, Instantaneous velocity, speed, velocity calculations are very useful if we consider it with day today life. If you learn how to calculate these then it will be very helpful for you to apply it in your day today life.
