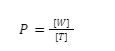Dimensions of Physical Quantities

The dimensions of any physical measurement or any quantity describe us about the composition of that measure. The dimensions of any physical quantity are just the first element we perceive whenever we look at it. In reality, our dimensions, such as length, height, and the quantity of muscle on our bodies, are likewise specified or noticed. An item’s dimension refers to how it may be measured in terms of basic variables. When we describe the dimension of a quantity, we are essentially defining its identification and presence. Everything else in the cosmos has depth, mass and volume, and hence has existence, this becomes evident.

Defining the dimensions of physical quantities

The values whereby the basic fundamental variables are elevated to express a parameter are described or defined as the particular quantity or parameter’s dimensions. The dimensionality of the seven basic fundamental variables or parameters is represented by parentheses.

General example/syntax,

The dimension of length or heights is denoted by [L], that of duration or time is denoted by [T], that of bulk or mass or we can say it as weight is denoted by [M], the electric current’s dimension is shown as [A], and that of any quantities is denoted by [mol]. Similarly, the dimension of temperature is [k], while [Cd] is the new luminosity strength dimension of light.

General formation of the dimension of a physical quantity

Imagine any physical quantity or variable M that is affected by some of its base quantities such as size or length, time, mass, the quantity of the substance, electric current and the temperature around it when increased to values or powers p,q,r,s,t,u and v. The dimensions of that particular physical quantity M may therefore be expressed as follows:

When writing the dimensionality of a parameter, we must use the symbol []. All of actual life is expressed given time, mass and length or size.

However, there is no need to learn the dimensions of any physical quantity and can be solved and found until we know the units or formula (for complex quantities known in simple physical terms) of that particular physical quantity. We’ll see further with examples of some quantities how we can derive them.

Some examples of the Dimensional formula

Force Dimensional Formula

Let us have a look at the dimensional formula of force. By having a look at the formula of force which is mass multiplied by acceleration,

F=M× a

Where, dimension of mass is [M] itself, dimension of acceleration can be taken by it unit which is m/s2.So its dimension will become as, [LT-2]. Where, L is the dimension of metre (represented as a length) and T is the unit of second (represented as time) and one can notice the power is also stated but with negative sign, so because the second is in the denominator in the unit of acceleration. 

So, the overall dimensional formula of force will be as,

In the following examples having the same approach we’ll see their dimensional formula with a quick look.

Power Dimensional Formula

In power, we know the formula of it is, the ratio of work to time. So, simplifying it as,

Energy Dimensional Formula

The energy can be of two kinds, potential energy and kinetic energy. Let us see the dimensional formula of both of them.
Kinetic Energy,

Similar to other examples its formula is ½ multiplied by mass multiplied by velocity, represented as, 

Conclusion

Dimensional formula of physical quantities or any physical parameter helps us to analyse the characteristics of that particular quantity or parameter. Or we can say it tells about the composition of the same. A dimensional formula of a complex quantity can be derived with the help of its formula and then their SI units. Few of them with examples of derivations are mentioned above. Such as the dimensional formula of power is [P]=[L2M1T-3], that of kinetic energy is [Ek]=[L2M1T-2], and similarly many are there.