When you dip chalk in water, the chalk slowly becomes wet as the water rises through its pores against the action of gravity. This happens due to the phenomenon of capillarity which is defined as the rise or fall in the level of liquid inside a capillary due to adhesive and cohesive forces. A Capillary is a narrow tube or porous solid through which a liquid can rise up or fall down. Cohesive forces are intermolecular forces between the liquid molecules. Adhesive forces are intermolecular forces between the liquid molecule and the capillary wall. It does not require the action of gravity.
Capillary Action
It is also known as wicking or capillary motion. In this, the liquid level ascends or descends through a capillary relative to its surroundings. Suppose we have a tub of water and we dip a capillary in it, then water will go in the capillary and rise through it.
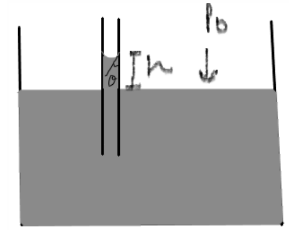
In the above figure, the water has risen through the tube under capillary action. When cohesive forces are smaller than adhesive forces, the liquid will wet the tube’s surface and a concave meniscus is observed. The angle of contact is less than 90o. The angle of contact is defined as the angle between the tangent to the liquid surface and the surface of the capillary.
The force by the surface tension of water acts in the upward direction and the force due to water’s weight acts in the downward direction. These two forces balance each other.
The upward force acting along the circumference = 2𝝅r ϒcos𝛳, where 2𝝅r is the circumference of the meniscus, ϒ is the surface tension of the liquid and cos𝛳 is the cosine of the angle of contact.
The downward force acting along the weight of the liquid = mg, where m is the mass of the liquid and g is the acceleration due to gravity
Mass of the liquid (m) = density (𝝆) x volume (V)
Volume of the liquid in capillary = 𝝅r2h, where h is the height by which the liquid has risen and r is the radius of the meniscus.
Hence, downward force = 𝝆 𝝅r2hg
Equating the upward and downward force gives 2𝝅r ϒcos𝛳=𝝆 𝝅r2hg
Rearranging the above equation, we get
ϒ=𝝆rhg cos𝛳/ 2
This is the equation for the rise of liquid in a capillary.
Capillary Rise Through External Pressure
When the liquid rises through the capillary and we get a concave meniscus, this is because the external atmospheric pressure is greater than the pressure inside the meniscus. Thus, the liquid will rise until the pressure becomes equal to the external pressure.

Factors Affecting Capillarity
Capillarity depends on various factors like the density of the liquid. If the liquid is denser, then the level of rise or fall of the liquid inside the capillary would not be as much as of a liquid with lower density.
The diameter of the capillary is also inversely proportional to the capillary action. More is the diameter of the tube, less is the capillarity.
Capillary action is directly proportional to the surface tension of the liquid.
Capillarity also depends on the angle of contact. If 𝛳<90o, then the meniscus will be concave and the liquid rises through the capillary and wets its surface. If 𝛳=90o, then there will be no rise or fall in capillary.
If 𝛳>90o, then we get a convex meniscus and liquid descends in the capillary. This happens when cohesive forces are greater than adhesive forces. The liquid does not wet the tube.
Capillarity is independent of the shape of the capillary.
When Capillary of Insufficient Length is Used
Suppose, to balance the external pressure, the liquid must rise by 5 cm in the capillary. However, we only have a capillary of 2 cm. Will the liquid spill outside? No. Physics works in interesting ways. In such a case, the angle of contact will change to account for the phenomenon. The radius of the meniscus increases, i.e., the curvature of the meniscus decreases.
Applications of Capillarity
Rise of oil through cotton wick used in diyas takes place due to the capillary action of threads in the cotton.
Plants get water through soil via capillary action.
A cloth or a towel soaks up water due to the capillarity of cotton threads.
In thin layer chromatography, the solvent rises up the chromatogram against the gravity because of capillary action of paper.
Ink is drawn to the nib of the fountain pen.
Conclusion
The definition of capillarity and it’s application were discussed in detail. A lot of everyday phenomena take place due to capillary action by the virtue of which a liquid rises up the capillary. It is based on the laws of physics that forces must cancel out each other. The weight of liquid in the capillary is balanced by the force due to its surface tension. Capillary action depends on a lot of factors such as liquid density, surface tension and angle of contact to name a few. If we can dry our body with a towel, we have capillarity to thank for it.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






