The force is said to be a natural existence or phenomenon that can cause a change in the motion or rest state of a body. Moreover, the force applied in the form of stress may cause a change in the dimension of the object. Hooke’s Law explained the principle of stress.  According to this law, the stress imposed on a body will be directly proportional to the strain causing that body. Hooke’s law postulated the spring’s constant, in which the spring length is increased as much as the force is applied to stretch it. Therefore, the spring constant is also called the force constant.

Force

An object which has constant restoring force regardless of displacement. This is derived from Newton’s second law of motion, which states:

The force is equal to the product of the mass of the body to that of the acceleration produced in the body. Therefore, the acceleration of a body is directly proportional to that of the force applied over the body. i.e., the greater the force will be applied, the greater will be the acceleration produced in the body. On the other hand, with the increase in the mass of the body, there will be a decrease in acceleration.

Constant Force

A constant force is defined as the force applied in a constant manner on a particular object in a direction parallel to that of the direction of the acceleration produced in the body.

As stated earlier, the constant force is directly proportional to that of acceleration produced in a body. Moreover, the direction of the constant force will be in the direction of the acceleration.

 This is justified by the formula given as:

h

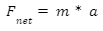
Force applied= mass of the object X acceleration

Examples of Constant Force 

  • Work done: Work done by a constant force is the work done by a constant force of 2 Newtons on an object having a mass of 3 kilograms.
  • Gravity: Motion of an object on the surface subjected to the pull of the earth’s gravity.
  • Pendulum motion: The motion of the pendulum is one of the common examples of constant force. The force applied over the pendulum does not change with 
  • Cycling: Cycling can also be considered as an example of constant force. In a condition, To keep the speed of the cycle constant, it is required to apply a force in a constant manner. Therefore a constant force is applied.
  • Buoyant force (Up-thrust): When a body is floating over liquid, it experiences a force of buoyancy, which acts in a constant manner to maintain the stability of the object over the liquid.
  • Intermolecular force: The force that is applied between the molecules is called the intermolecular forces. These intermolecular forces are applied in a constant manner so as to maintain the stability of the molecule.

Dimensional Formula

When a physical quantity is equated with its dimensional formula, it is an expression that denotes the powers to which the fundamental units are raised to obtain a unit of a derived quantity.

In mechanics’ mass, length, and time are selected as three base dimensions from which other derived quantities such as velocity, force, energy are derived. The fundamental units are expressed as

Length expressed as ‘L.’

Mass expressed as ‘M.’

Time expressed as ‘T.’

 Together they are represented as [ M L T]

Dimensional Formula of force

Force= mass x acceleration. Substituting this in the formula of force we get

F= M x M0L1T-2

Therefore,

F= M1L1T-2

Now computing the dimensional formula of force:

Derivation

Force Constant= Force × [Displacement]-1 . . . (1)

Since, Force = m × a

Therefore, The force is represented as,  [M1 L1 T-2] . . . (2)

And, the displacement is represented as,  [M0 L1 T0] . . . . (3)

Putting the value of equation (2) and (3) in the equation (1).

Force Constant= Force × [Displacement]-1

= [M1 L1 T-2] × [M0 L1 T0]-1 = [M1 L0 T-2].

Therefore, the dimensional representation of the constant force is, 

 [M1 L0 T-2]

 The dimensional formula of force constant is given by,

[M1 L0 T-2]

Where,

  • M = Mass
  • L = Length
  • T = Time

Conclusion

A constant force is defined as the force applied in a concerted manner over an object. At the same time, the direction of the constant force is parallel to that of the direction of the acceleration produced in the body. However, the work done by a constant force is denoted by the product of the acceleration produced in the body as well as the force applied on the body.

It is denoted by W = F.d.

It is equal to the force’s magnitude multiplied by the distance the item travels in the force’s direction.