Magnification is the process of expanding the actual size or dimension of a variable in general terms. The magnification provided by a lens is termed as the ratios of the image height to the object height in optics.
The magnification factor is calculated as the ratio of size of the produced image to size of the actual objects, as shown in the formula below.
M = – (S2/ S1) = f/ f – S1
where
The magnification factor is M.
The image’s size (height) is S1, and the object’s size is S2.
If the created image is actual or virtual, the negative sign indicates it. The magnification of virtual pictures is positive, whereas the magnification of real images is negative.
Derivation of the Formula
Consider the object OO ′, which is positioned on the primary axis with its height perpendicular to it, as illustrated in Fig. The ray OP will not deviate as it passes through the optic centre. The ray O ′A must pass through the focus F2 to be parallel to the primary axis.
The intersection of O ′PI′ and AF2 I′ creates the image. Draw a perpendicular to the primary axis from I′. This is the perpendicular II ′.
OO ′ is represented by the image.
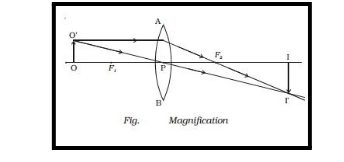
The ratio of the image’s size to that of the object is known as linear or transverse magnification.
Magnification m = Image Size / Object Size = II?/OO? = h2/h1 Magnification
where h1 denotes the object’s height and h2 denotes the image’s height.
We get II?/OO? = PI/PO from the identical right angled triangles OO′ P and II′ P.
Using the sign convention,
-h2 = II′
+h1 = OO?
+v = PI
-u = PO
We get magnification by substituting this into the above equation.
M=-h2/+h1 = +v/-u
M=+ v/u
For a real image, the magnification is negative, but for a virtual image, it is positive. It is always positive in the case of a concave lens.
The equation for magnification can alternatively be calculated using the lens formula as follows:
m = h2/h1 = v//u = (f-v)/f = f/ (f+u)
This equation holds true for real and virtual images, as well as convex and concave lenses.
Lens Formula
Convex lenses are also called converging lenses because the rays of it converge when they pass through them, whereas concave lenses are known as diverging lenses as the rays diverge when they pass through them. Based on their proximity from the lens, these lenses can create virtual or real images, and they can be of various sizes. By using lens formula and information of the distance of the object and the focal length, an distance of the image can be determined. In optics, the Lens formula expresses the relation between the image distance and the distance of the object (o), and the focal length of lens.
1/i + 1/o = 1/f
i denotes the distance of the image from the lens
o denotes the distance of the object from the lens
f depicts the focal length of the lens
With appropriate sign conventions, the lens formula can be used in any context. This lens formula works for both concave and convex lenses. The image is a virtual picture on the same side of the lens as the object if the equation yields a negative image distance. If the focal length in this equation is negative, the lens is a diverging lens rather than a converging lens. This equation can be used to calculate the distance between real and virtual images.
Magnification with the help of lens Formula
The ratio of the height of an image to the height of an object is defined as the magnification of a lens. It’s also expressed in terms of picture and object distances. It equals the image distance divided by the object distance.
M is equal to height of the image divided to the height of the object
The height of the object is always positive as it is always directly above the axis of the principal. However, subject to the kind of the image formed, the indicator for image height may change. Images that are virtual should have a positive height, while images that are of the real world should have a height that is negative.
The Convex Lens magnifies the image
Because a convex lens can create both virtual and real images, the magnification it produces might be positive or negative.
For a virtual image, magnification is positive, but for a real image, it is negative.
The image is magnified when |m|>1.
The image is diminished when |m|<1 is used.
When |m|=1, the picture and the object are the same size.
Magnification produced by a Concave Lens
Because concave lenses always produce virtual pictures, their magnification is always positive. As the image formed by a concave lens is always smaller than the object, |m|<1.
Conclusion
In general, magnification is the process of increasing the size or dimension of a variable. It also has various application be it a magnifying glass with a convex lens that allows the user to hold objects closer to their eyes to make them appear larger or a telescope that creates an image of a distant object with its huge objective lens or primary mirror and then allows the user to view the image closer with a smaller eyepiece lens, making the item appear larger.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






