Profile
Settings
Refer your friends
Sign out
Instantaneous acceleration is the acceleration that has a time limit nearly to zero and thus it helps us to calculate the value at an instant. The formula for instantaneous acceleration will help us to know about acceleration at a specific instant or can be said at a specific time interval. Now let’s discuss acceleration, the formula for instantaneous application, average acceleration and instantaneous application in a derivative manner.
Acceleration and Average acceleration
The rate at which velocity changes using both speed and direction with respect to time is called Acceleration.
Formula:
The formula for acceleration is
ā = ∆v / ∆t
Where;
∆v = V – Vo
V = final velocity
Vo = starting or initial velocity
ā = average acceleration
t = time
The rate at which velocity changes using both speed and direction with respect to time at a particular interval is called average acceleration.
Formula:
The formula for average acceleration is
Instantaneous Acceleration
Instantaneous acceleration is the rate at which velocity changes using both speed and direction with respect to time such that the time interval goes to zero.
Formula:
The formula for instantaneous acceleration is :
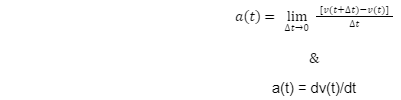
Derivation of the formula of Instantaneous acceleration
Instantaneous acceleration is the Average acceleration between two points that approaches a time limit of nearly zero. To find the formula for instantaneous acceleration we will go through the same basic formulas and from that, we will derive the instantaneous acceleration of any particle or anything moving particles.
Now we will use the general formula to determine the formula of instantaneous acceleration from the average acceleration with a time limit of nearly zero.
First, Expressing velocity (v) is a continuous function of time (t) and is denoted as v(t).
Now the average acceleration we know is ;
a = [v(t2) – v(t1)] / (t2-t1)
Now we need to find acceleration at any position so let, t1 = t and t2 = t+ ∆t and we know ∆t should be nearly zero so to calculate instantaneous acceleration putting ∆t nearly zero we will get
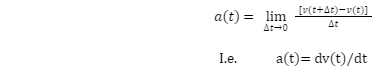
This is the required formula for instantaneous acceleration.
Some Solved Examples
Q1) The position of a particle is x(t) = 2t + 0.7t³ m. Find the instantaneous acceleration at t= 3 sec?
Ans: we have,
x(t) = 2t + 0.7t³
So,
v(t) = dx(t)/dt = 2+2.1t² m/s
Now,
a(t) = dv(t)/dt = 4.2t m/s²
Therefore,
At t = 3 sec instantaneous acceleration is;
4.2t = 4.2 × 3= 12.6 m/s² (Answer)
Q2) A particle is in motion and is accelerating. The position of the velocity is v(t) = 10t – 3t² m/s
- Find the functional form of acceleration.
- Find the instantaneous velocity at t= 1,3,4,5 s
- Find the instantaneous acceleration at t= 1,3,4,5s.
- Analyze the results of © in terms of acceleration and velocity vectors directions.
Ans: we have,
v(t) = 10t – 3t² m/s
- a(t) = dv(t)/dt = 10 – 6t m/s²
- v(1s) = 7 m/s
v(3s) = 3 m/s
v(4s) = -8 m/s
v(5s) = -25 m/s
- a(1s) = 4 m/s²
a(3s) = -8m/s²
a(4s) = -14m/s²
a(5s) = -20m/s²
At t = 1 sec, we have the velocity v(1sec) = 3 m/s which is positive; so both velocity and acceleration will be positive and in the same direction.
At t = 3 sec, we have the velocity v(3 sec) = 7m/s which is positive; so both velocity and acceleration will be positive and in the same direction.
At t = 4 sec, we have the velocity v(4sec) = -8m/s which is negative; so both velocity and acceleration will be negative and in the opposite direction.
At t = 5 sec, we have the velocity v(5sec) = -25m/s which is negative; so both velocity and acceleration will be negative and in the opposite direction.
(Answer)
Q3) The position of a particle is x(t) = 2t² + 0.7t m. What will be the instantaneous acceleration at t = 2 sec ?
Ans: we have,
x(t) = 2t² + 0.7t
So,
v(t) = dx(t)/dt = 4t+0.7m/s
Now,
a(t) = dv(t)/dt = 4t m/s²
Therefore,
At t = 2 sec instantaneous acceleration is;
4t = 4× 3= 12m/s² (Answer)
Conclusion
Instantaneous acceleration, average acceleration and formula for instantaneous acceleration plays an important role in day-to-day life. And it will help you to calculate acceleration at some instant which will help you to know how important this is and you will find applications of these things in different stages of life.
