Profile
Settings
Refer your friends
Sign out
The energy of an electron changes when it jumps from one atom to the next. A photon of light is produced when an electron goes from a high to a lower-energy orbit. The atom consumes a photon of light when an electron goes from a low energy level to a higher energy level. Rydberg’s constant (abbreviated as R∞) is a basic constant of atomic physics given by Swedish physicist Johannes Rydberg, who identified the wavelengths of light in various sequences of related spectral lines, most notably those emitted by hydrogen atoms in the Balmer series.
For hydrogen, the constant is RH, and at the limit of infinite nuclear mass, it is R∞. In both ways, the constant is used to assert the lowest-energy photon able to ionise an atom from its ground state or the highest wavenumber of any photon that may be emitted by an atom. The Rydberg constant for hydrogen RH and Rydberg’s constant formula can express the hydrogen spectral series.
The atomic spectrum of hydrogen, as well as a variety of other atoms and ions, is explained by the Bohr model. It is not exact, but in many circumstances, it is a very good approximation, and it has historically played a central role in the development of quantum theory. According to the Bohr model, electrons orbit around the atomic nucleus similarly to how planets revolve around the sun.
Rydberg’s Constant Formula:
The infinity sign is chosen because the light released by the atom’s nucleus is extraordinarily large compared to a single revolving electron. Rydberg’s constant formula can be expressed as:
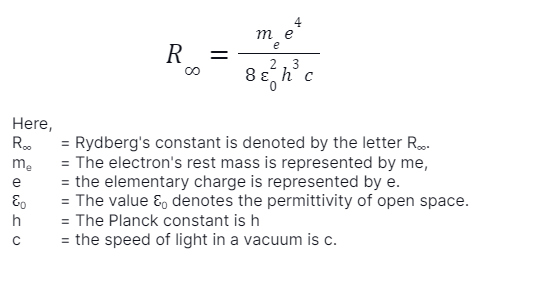
Rydberg’s constant R∞ has a value of 10,973,731.56816/metre. When this form is used in the accurate explanation of a sequence of spectral lines, the result equals the number of waves each unit length or wavenumber. The frequencies of the spectral lines are attained by multiplying with the speed of light.
In the spectroscopy field, Rydberg’s constant is a constant connection to atomic spectra. Heavy atoms are denoted by the letter R, while RH denotes hydrogen. Rydberg’s constant first appears in Rydberg’s constant formula as a fitting parameter. Neils Bohr used essential constants to determine it later.
Bohr’s Theory Of Hydrogen Atom-Rydberg’s Constant:
Let us first know what Bohr’s theory of hydrogen is:
Bohr’s atom model provides a very logical explanation of the existence of a large number of lines in the atomic spectrum of hydrogen. According to Bohr’s theory, when an electron is excited from a higher energy level to a lower energy level, it emits energy. The emitted energy is quantized and corresponds to a definite frequency or wavelength. It forms the basic existence of many well-defined lines in the atomic spectrum of hydrogen.
The energy state corresponding to the minimum energy is termed the ground state. A hydrogen atom contains only one electron in the shell, the ground state. When a hydrogen atom is provided with energy from an external source, the electron present in the ground state gets excited and jumps to a state of higher energy. This state is termed the excited state. The excited state is very short-lived and has a lifetime of about 10-8seconds. Therefore, the excited electron cannot stay longer in the excited state. As a result, it is forced to drop to a lower energy level.
The Rydberg constant formula describes the wavelength of light produced by an electron travelling between energy levels within an atom. The following formula was derived from Rydberg’s observations and Bohr’s atomic model:
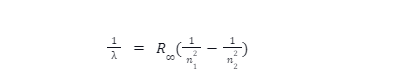
Where, n1 and n2 are integers, with n2 being greater than n1. It was later determined that n1 and n2 are related to the energy quantum number.
Conclusion:
During his investigations of spectral series, Swedish physicist Johannes Robert Rydberg employed wavenumbers instead of wavelengths in his calculations. He arrived at the simple expression with a constant term while conducting the calculations. The term “constant” was later shortened to “Rydberg Constant.” The wavelengths in the hydrogen spectrum are evaluated using this constant. A photon is formed or released when the binding energy is converted to the transverse form, expressed in the Rydberg constant. The Rydberg constant is measured in wavelengths and frequencies. This constant can be used to compute the wavelength of various spectral series.
