Profile
Settings
Refer your friends
Sign out
The moment of inertia is a vector quantity of an object which is under rotational motion. Angular momentum, on the other hand, is the quantity of a body under rotation, which is the product of its angular velocity and its moment of inertia. The symbol of the angular
In this article, we will learn about the basic concept of moment of inertia, the angular momentum of a particle, and other related topics. Angular momentum of a particle is an important part of the moment of inertia which comes under physics, a branch of science.
Let’s start the article with the moment of inertia.
Moment of inertia
It is a calculated measurement of a rigid body under rotational motion. In simple words, the moment of inertia measures the difficulty of changing the body’s rotation speed at a fixed time. Rotational inertia, the mass moment of inertia, and the second moment of mass and angular mass are the other names of the moment of inertia. Resistance of an object to alter the angular acceleration is a quality of the moment of inertia. The calculation of moment of inertia identifies the force it would take to speed up, slow, or stop the rotation of an object.
Some simple examples of moments of inertia are the pendulum, dial of the telephone (old or vintage landline phone with a rotating dial), etc. We can calculate the two key quantities i.e., rotational kinetic energy and angular momentum, through the moment of inertia.
Where
M = mass of the particle
r = distance from the rotation axis
What is the angular momentum of a particle?
Angular momentum of a particle can be defined as the property of some rotating object, which is calculated by the product of angular momentum and the moment of inertia of that rotating object. Angular momentum is a vector quantity that contains both direction and magnitude. It can be referred to as linear momentum.
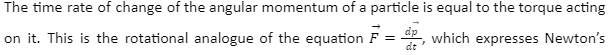
second law for the translational motion of a single particle.
Angular Momentum of a Particle formula
Let us consider a linear momentum p with a particle of mass m at a position r in relation to its origin O. Here, angular momentum L for a particular particle in respect to its origin O is defined to be:
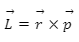
The angular momentum magnitude vector is-
L = rp sinθ
Where,
p = magnitude of the momentum
r= position of the object
= the angle between r and p
Example of angular momentum:
Earth has an angular momentum on its orbit, which is named orbital. As the earth revolves around the sun annually and spins with an angular momentum on its axis, we experience the phenomenon of alternating days and nights.
Different sports use angular momentum to spin the ball, which is generally rotated as it is bounced or thrown. These include baseball, volleyball, and basketball. The bat in baseball picks up angular momentum as it is swung, transferring most of the momentum to the ball when the contact takes place.
Angular momentum quantum number – Definition
It is also termed as the secondary quantum number defined as the quantum number for an atomic orbital that decides on the angular momentum and also defines the shape or size of an orbit. Basically, the value of a secondary quantum number varies from zero to one.
Conclusion
The magnitude of the object’s angular momentum is equal to its linear momentum and at the r (perpendicular distance) from the rotation’s centre to a line drawn in the direction of its immediate motion and passing through the object’s centre of gravity. In the above article, we have defined the topic of a moment of inertia, the angular moment of a particle, its formula and other related topics. For a better understanding of the angular momentum, we have described the example.
