Acceleration is the ratio of change in Velocity to the time taken. It is represented by the formula ‘a’. It has the SI unit as m/s2 .Acceleration is a vector quantity and therefore it depends on both the magnitude and direction of the object under consideration.
Formula for Acceleration
Acceleration is the change in Velocity divided by the time taken or the other definition of acceleration is rate of change of velocity.
The formula for Acceleration is as follows -:
a = change in Velocity / time taken
Here, a= acceleration in the unit m/s2.
Velocity with the unit- m/s
And time in the unit – s
a = m/s*s = m/s2 as the SI unit of acceleration.
Uniform Acceleration
Uniform Acceleration is when an object travels in a straight line and the velocity of the object increases or decreases by an equal amount in equal intervals of time. Then we say that the body or object is uniformly accelerated.Examples of Uniform acceleration are – The motion of a body under free fall, bicycle going down a slope, skydiver jumping out of plane.
Non- Uniform Acceleration
Non- Uniform Acceleration is when an object or a body if the velocity increases or decreases at an unequal or non – uniform rate.Examples of Non – Uniform acceleration – A car travelling on the road changes its velocity by unequal amount in equal interval of time it is known as non- uniform Acceleration.
Acceleration of a body on a Smooth Horizontal surface
CASE -I
Let us take a block of mass ‘m ‘ resting on a Smooth Horizontal surface and an unbalanced force ‘F ‘ is applied on the body in the horizontal direction then the body will move with an acceleration ‘ a.
Forces acting on the block are as follows -:
- The gravitational force due to its weight is acting downwards, which is equal to the mass of the object multiplied by the ‘g’ that is Acceleration due to gravity. That gives us ‘mg’ acting downwards
- Reaction force ‘R’ acting perpendicular to the block-balancing mg. The reaction force acts upward.
- The unbalanced force ‘F’ acting in the horizontal direction.
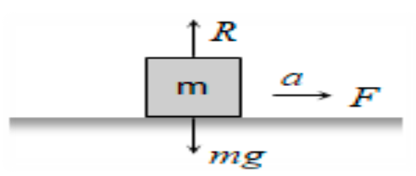
The net equations are as follows -:
mg and R are balanced therefore
mg =R ————————————(1)
And since F acts in the horizontal direction Hence, F= ma —————————–(2)
Where m = mass of the block
a = Acceleration produced due to the unbalanced force
F= Force applied
From equation (2) we get -:
a= F/m
Hence acceleration on a Smooth Horizontal surface is given by
Acceleration = Force / mass of the object
CASE -II
Now consider if the force acts at an angle of theta θ in the upward direction as shown in the figure-:
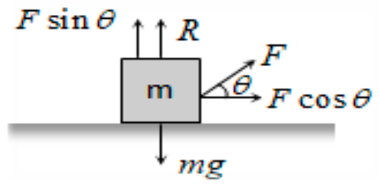
Here Force ‘F’ can be broken down into two components ‘ F cosꝋ ‘ and ‘ F sinꝋ ‘. The horizontal component is F cosꝋ while the vertical component is F sinꝋ.
- The forces that act on the block are the Reaction force
- mg acting downward and Fsinꝋ force component acting in horizontal direction and F cosꝋ vertical direction.
Hence in upward direction we have the Reaction force R followed by the F sinꝋ which is balanced by mg
Therefore, mg = R + F sinꝋ —————-(1)
Similarly, in the horizontal direction
Fcosꝋ = ma —————-(2)
From (2) we get a= F cosꝋ / m
That is Acceleration = F Cosꝋ / mass of the object
CASE – III
In the third case we consider the Force ‘F’ acts in a downward direction as follows-:
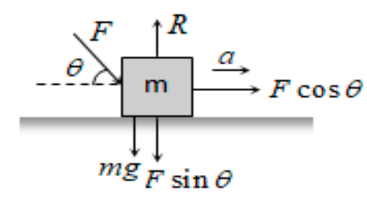
Now in this figure the force acting on the block are as follows -:
- The Reaction force ‘R ‘ acting upward, mg acting downward.
- F sinꝋ acting downward and F cosꝋ acting horizontally as seen.
balancing the forces in both directions
We get Reaction force = mg + F sinꝋ
R = mg + F sinꝋ —————————–(1)
While in the horizontal direction
F cosꝋ = ma ———————————–(2)
From equation (2) we can say that
a= F cosꝋ / m
Or we can say
Acceleration = F cosꝋ / mass of object
Acceleration Due to gravity
Earth’s gravity is represented by a symbol ‘g ‘. This the value of acceleration due to gravity and the centrifugal force that acts on a body. Being a vector acceleration due to gravity depends on both the magnitude and direction. Similar to Acceleration, it has the SI unit as m/s2 and is also equivalent to Newton per kilogram.
The value of acceleration due to gravity of any object or body is around 9.81 metre per second squared.
This value comes out after ignoring air resistance and the object is considered to be in free fall. Further the value of acceleration due to gravity varies based on the height above the surface, depth of the object, latitude and so on.
Conclusion
Acceleration is defined as the rate of change of velocity with time or the change in velocity in a given time. Acceleration is a vector quantity and depends on both magnitude and direction. The SI unit of acceleration is metres per second square – m/ s2. Acceleration can be uniform Acceleration or Non – uniform. Further acceleration on a Smooth Surface can be calculated by breaking the force acting into various components and then balancing the forces to get the value. The earth also has a force that it exerts on everybody on its surface; this force that is experienced by everyone is known as gravity and the acceleration produced due to this is known as Acceleration due to gravity represented by ‘g’. The value of g varies with height, depth and altitude. On earth the Value of Acceleration due to gravity is around 9.81 metre per second squared.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






