The vector product, also known as the two vectors’ cross product, is a new vector with a magnitude equal to the product of the magnitudes of the two vectors into the sine of the angle between these. If you use the right-hand thumb or the right-hand screw rule, the direction of the product vector is parallel to the direction that has the two vectors in it.

Cross Product of Two-Vectors

When two vectors are crossed, they are multiplied by each other. The sign (x) denoting a product (cross) is placed between two vectors. It is a three-dimensional binary vector operation. A third vector, which lies in the perpendicular direction of two originals, is formed by taking the two original vectors’ cross product. The parallelogram’s area is the one that connects them determines its magnitude, and the rule of the right-hand thumb can be used to calculate its direction. Because the cross-product of vectors gives rise to vector quantities, it’s sometimes referred to as a “vector product”. The two vectors’ cross product is the subject of today’s lesson.   

A few key points of cross products:

  • Cross product is a type of multiplication of vectors in which two vectors of distinct natures or kinds are multiplied. 
  • The direction and the magnitude of a resultant vector are both present. By using the dot and cross product, two or more vectors can be multiplied.  
  • The vector obtained is referred to as the two vectors’ cross product or the vector product when you multiply the vectors, such as two or more, with each other and the vectors’ product is likewise a vector quantity.  
  • The resulting vector is perpendicular to the plane in which the two provided vectors are located.

Understanding a cross vector

For example, if there are vectors (two) that lie in a plane (X-Y), their cross product will produce a vector obtained in the Z-axis’s direction, which is perpendicular to the XY plane. Between the vectors that are original, we use the x symbol. The product of the vector often referred to as the cross product of these two vectors, looks like this: 

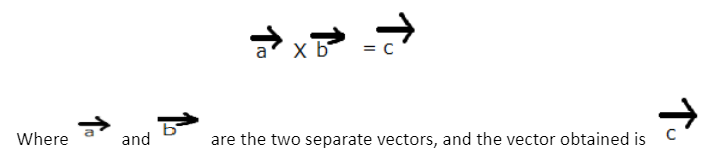
The following are some essential considerations:

  • The angle formed by a and c is 90 degrees always. a and c are thus the vectors known as orthogonal. 
  • The angle formed by both C and B is always 90 degrees. 
  • C as well as B, in other words, are vectors that are orthogonal.
  • We can make the resultant vector a zero vector by placing a and b in a parallel direction towards each other or at a 0° angle.
  • The vectors (which are the original ones) must be parallel (at a 90° angle) to obtain the biggest magnitude, as the vectors’ cross product (two of them) must be the maximum. 

The formula for two vectors’ cross product

If we take two vectors, for instance:

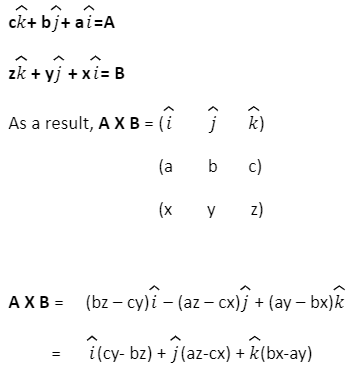
Cross Product: The Right-Hand Rule

  • The right-hand rule can be used to determine the direction of the unit vector. 
  • We can stretch our right hand so that the index finger points towards the first vector’s direction and the middle finger points in the second vector’s direction using this rule. 
  • The direction or unit vector n is then indicated by the right hand’s thumb. 
  • We may simply demonstrate that the cross product of vectors is not commutative using the right-hand rule. 

For instance, there are A and B, which are a couple of vectors, then the diagram for the rule of right-hand thumb looks like this:

 

The properties of Cross Product

 We may utilise properties to find the two vectors’ cross-product. To obtain the two vectors’ cross product, features such as anti-commutative property and zero vector property are important. Other properties include the Jacobi property and the distributive property, among others.   

The following are the properties of cross-product:

(i) The two vectors’ cross product has a length equal to:

 → →

 a × b = |a||b|sin(θ) 

 

(ii) The property of anti-commutative is:

→ →     →  →

a× b=  −b × a 

(iii) The Distributive property is:

→   →   →      →   →       →   →

a × (c + b) = ( a  ×  b )+ ( a  × c) 

(iv)The zero vector’s cross product:

→    →     →

a   × 0  =   0  

(v) The vector’s cross product with itself:

→   →    →

a   × a  = 0  

(vi) When a quantity (scalar) is multiplied, the result is:

→  →       →      →       →     →        →

c    (a   ×   b)=   (c a)   ×  b  =  a   × ( cb) 

(vii)The unit vectors’ cross product is:

→   →       →     →       →    →

i   ×  i   =   j   ×   j      =  k  ×  k =  0  

Conclusion

We have learned about the vector product, cross vector, its properties, and the right-hand rule with different examples and formulas. Here are a few key pointers to keep in mind:

  • The right-hand thumb rule determines the direction of the vectors’ cross product.
  • The magnitude is determined by the area of the parallelogram created by 

→        →

a   and b;  the original two vectors.    

  • A zero vector is the cross-product of a couple of linear or parallel vectors.