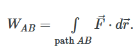Vector Algebra – Work Done By A Force

Vector Algebra

What is Work Done by a Force? Work is done when a force of specific magnitude acts on an object and causes displacement from its initial position to another position. Forces acting on the object can vary as a function of position. The object’s displacement can also occur along various paths between its initial and final points. 

How do you measure the work done by the force acting on the object? Begin by defining the work increment as “dW” done by a force F operating through the infinitesimal displacement dr as the dot product, as illustrated below:

It is the dot product of these two vectors, namely the force acting on the object and the change in displacement that occurs due to the application of the force. 

Once you calculate the contributions for infinitesimal displacements individually, it is time to find the cumulative of these values. Finally, add all the values along the path between the initial and final positions of the object due to the application of the force. The resultant of the summation of these displacement values will give the total work done by a force. 

Calculating the work done by a force

The work done due to the application of force on the object is the integral sum of the forces of different magnitude with respect to the displacement occurring throughout the pathway. The numerical representation of the formula is:

Let’s define this formula with an elaborate example below. 

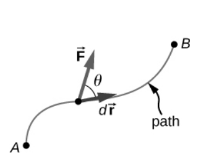
We have used vector algebra to illustrate the work done on any object due to the application of force. Vectors are used for defining work. Compare the image and the explanation here:

The force acts on a particle and causes the tiny displacement from one point at A to another at B. The small work will be the dot product of these two vectors along the path shown by the arrow in the image.

So, here the work done on this particle depends on both the force and the distance it travels due to the force. So, when using vector algebra, be specific about the values of both the force and the distance traversed by the body, along with the directions. Here, find the direction of the resultant force acting on the body, represented by the blue arrow.

Using the dot product of these two vectors, force and displacement, find the accurate value of work done on the object. Here the product of two vectors force and displacement is calculated by the formula:

W= F. d cos (𝜃)

Where,

F = magnitude of the force acting on the body

𝑑 = magnitude of the body’s displacement due to the force acting on it

𝜃 = the angle between the directions of 𝐹 and 𝑑

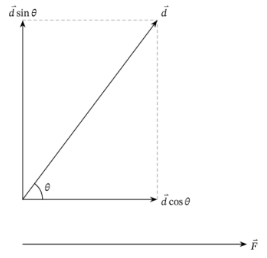
Here, the graphical representation clearly shows the directions of displacement and force acting on the body. Determine the angle between the two vectors to evaluate the total work down on the object by the acting force.

Let’s take a close look at an example to use this formula and determine the total work done by the force:

Example 1: 

A body moves across the place, where the vectors “a” and “b” are perpendicular unit vectors. A force F = (9a+b) N acts on the body and moves it from the initial position with the position vector (-9a+6b) m. Find what is work done by a force F.

Answer:

The work done on the body by the force F will be the dot product of the vector force and displacement acting on the body. The displacement is not given in the question, but it the position vector is given. According to the question, the body moves to the stated position from its original point. Therefore, the displacement of the body is given by:

d= {(9-9-0) a+ (6-0) b} m which is equal to the position vector.

Therefore, the work done, W= Dot product of F and d

= (9,1).(-9,6)

= (9*-9) + (1*6)

= -81+6

= -75

So, the total work done, W= -75J

The work done here is negative. So, the body’s energy is conserved only if the kinetic energy decreases. If not conserved, it will increase the body’s potential energy.

Example 2: 

A force of 14 N acts on an object and causes displacement of 8m in the direction of the force acting on it. What is the work done on this object?

Answer:

Force acting on the object, F= 14 N

Displacement of the object that occurs from the initial position to final due to the force is d= 8m

Therefore,

Work done on the object= 14 N * 8m

= 112 J

The work done is 112J on the body in the direction of the force and displacement.

Key points to remember

• The work done on any object by a constant force over a specific displacement will be the dot product of the force and displacement vectors.
• The dot product is calculated by considering the angle between the two vectors, force and displacement.
• The dot product can be determined without using the angle and expressing the force and displacement vectors in the component form.
• If the components, force (F) and displacement (d) are in the perpendicular directions a and b, then