We usually interact with quantities that have magnitude and direction in our day-to-day lives. Examples of such quantities could be displacement, velocity, acceleration, force, etc. These quantities are known as ‘vector quantities’ and are further classified as vectors in two and three dimensions.
Vectors: Meaning and Definition
Rahul posted on social media that he was going on a road trip and travelling 200 km from home, but it was unclear where he was headed. An aeroplane is flying at 650 Km/hour, but is that information enough to know about its destination? Similarly, while launching a missile, the operator needs to know the direction and angle towards which they have to launch their target.
In situations where only numerical value (magnitude) is considered without mentioning any direction, they are called scalar quantities. However, in all of the above situations, the numerical values – 200 km, 650 km/hour, and the angle does not provide complete information.
We need to know the direction of Rahul’s motion in case 1; is he going from Delhi to Haryana, Ambala to Amritsar, or Shimla to Manali? We need similar information on direction in case 2 of the aeroplane’s flight and case 3 of launching a missile.
In our day-to-day lives, we usually interact with quantities that have magnitude and direction. Examples of such quantities could be displacement, velocity, acceleration, force, etc. These quantities are known as ‘vector quantities’ and are further classified as vectors in two and three dimensions.
Vectors in 2-D and 3-D
A vector means a quantity that has both a magnitude and a direction. We can picture a vector as a directed line segment(→), whose length represents the magnitude of the vector and with an arrow indicating the direction. The direction of the vector is from its tail to its head.
The vectors can be represented in two as well as in three dimensions. A two-dimensional vector can be represented using its mutually perpendicular components in x and y directions; this tells us how far the vector goes in each direction. E.g., a vector with an x-component 3 and a y-component 5 that started at the origin would end at coordinates (3,5).
The magnitude of a vector is the total amount of the quantity represented by the vector. For a two-dimensional vector, the magnitude is equal to the length of a triangle’s hypotenuse in which the sides are the x- and y-components. Therefore, if we want to know the two components of the vector and want to find the magnitude, we can apply the Pythagorean Theorem.
Basic Introduction to Vector Calculations
Let’s understand the significance of vectors in daily life with the help of a basic example:
Force: Observe the given figure where a box is being pulled in two opposite directions:
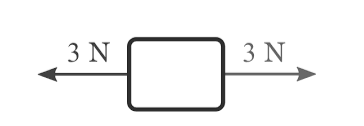
3 Newton (N) force pulls the box in the left direction, and 3 N force pulls the box in the right direction. Now, the net force on the box will be 3 – 3 = 0 N . Hence, the box will not move as the total force acting is 0 N.
The above example depicts the significance of considering directions while doing calculations in some quantities (which we call vector quantities)
Displacement: Imagine Pradeep is walking in a garden, from point A to B and then B to C. The total distance covered by Pradeep is 20 m. However, the actual displaced length is only AC.(fig. 2). We will not merely add AB and BC but apply the Pythagoras theorem to calculate AC to find out the displacement.
Let us explore the different types of vectors.
Types of Vectors in Mathematics
Zero vector: When the initial and final position is the same, the actual distance between the two points becomes zero; such a vector will be called a zero vector.
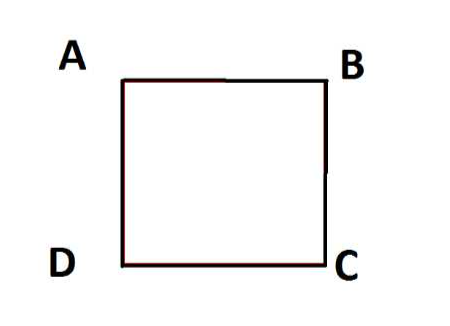
Example: In fig. 3, let a person walk in the given direction A —>B—>C —> D → A. Since the initial and final points of the person are the same, the actual displacement of the person will be zero.

Unit vector: Any vector whose magnitude is one will be called a unit vector.
Co-initial vectors: When two or more vectors have the same starting point, they are co-initial vectors.
Collinear vectors: These vectors are either parallel to each other or parallel to the same line.
Equal vectors: These vectors have exactly the same magnitude and direction.
Like vectors: These vectors have the same direction.
Unlike vectors: These vectors have opposite directions.
Coplanar vectors: These vectors lie in the same plane.
Conclusion
The vector represents the quantities involving directions. Wherever there is a movement, there is a type of vector involved. These are fundamental quantities by which various predictions and analyses related to the weather, projectile movement, flow of liquids, etc.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






