Profile
Settings
Refer your friends
Sign out
A vector is a type of object with both a magnitude and a direction. So if we geometrically take it, it can be thought of as a directed line segment where the length is the magnitude, and the arrow indicates the direction.
In this article, the main point of our discussion would be vector geometrical problems, the operation of vectors, and the concept of magnitude and direction of a vector.
Representation of Vectors
Since you now understand vectors, if two vectors are the same, they would have the same magnitude and direction. If we take a vector and change it to a new position without rotating it, the vector we obtain will be the same as we get initially.
We generally denote vectors as in a or b. The magnitude of a vector can be indicated by a or || a ||
Let us now understand
Magnitude and direction of a vector
Here the blue arrow represents a vector named a. So the main properties of a vector, magnitude and direction are given by the red bar and green arrow.
So, as you can see, the red bar’s length is the magnitude || a || of the vector a; the green arrow has a length of 1, but the direction is the direction of vector a.
The length is always one except in the case of zero vector as it has zero magnitudes, and the direction is also not defined.
So even if you change the position of a, it will not change the vector because its magnitude and direction remain unchanged.
Exception of a Vector
One of the essential exceptions of a vector is the zero vector, denoted by 0. Since it has no length, it does not point in any particular direction, thereby having an undefined direction.
Operations on Vectors
We can define various vector operations geometrically without any reference to the coordinate system. This article will mainly focus on the addition, subtraction, and multiplication of a scalar.
Addition of Vectors
Let us understand the addition of two vectors.
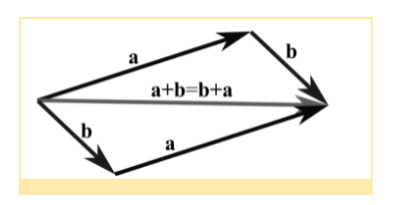
With reference to the above diagram, there are two vectors, a and b, and we add them and get the sum as a+b. The vector b is translated until it coincides with a, and we know that translation does not change the vector.
So, the directed line segment from the tail of a to the head of b is the vector a + b.
The addition of the vector is the way the forces, as well as velocities, combine.
Let us take an example.
Suppose a bus is traveling north at about 20 miles per hour and a child seated just behind the driver throws a ball at 20 miles per hour to his brother sitting east of him. In that case, the velocity will be in a northeasterly direction.
The velocity vector will form a right triangle where the total velocity becomes the hypotenuse, and hence the total speed of the object, which is the magnitude of the velocity vector, is 202 +202= 202
The addition of vector satisfies the two most important properties,
- The commutative law, which states the order of addition does not matter
a + b= b+ a
It is also known as the parallelogram law, where one of the edges of a parallelogram defines a + b, and the other pair represents b+ a. Both the sums are equal to the same diagonal of the parallelogram.
2.Associative law states that the sum of three vectors does not depend on which pair is added first.
(a + b) + c = a + (b + c)
Subtraction of Vector
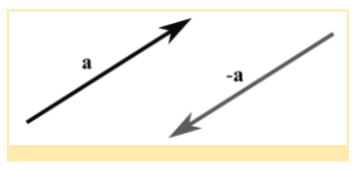
Before we define subtraction, let us first define vector – a that is the opposite of a. The vector -a is the vector with the same magnitude but pointed in the opposite direction.
Generally, we define subtraction as the addition but with the opposite of a vector
b – a = b + (-a)
Now, this is equivalent to turning a vector a. So if you see in the diagram below, you will understand that vector x in the figure is equal to b – a. It is pretty as similar to stating a + x =b
Scalar Multiplication
If a vector a and a real number that is scalar λ, then we can form the vector λa as follows
If λ is positive, then the λa will be in the same direction as the length would be λ times the length of a. In this case, the λ stretches (if λ>1) or compresses (if 0< λ<1) the vector a.
If λ is negative, we take the opposite of a before we stretch or compress a.
Whatever the sign of λ we are observing that the magnitude of λa is | λ | times and the magnitude of a: || λa ||= | λ|||a||.
Conclusion
This article discussed the definition of vectors, vector addition, vector subtraction, and different geometrical problems through vectors without using coordinate geometry as reference.
The advantage of a vector using geometrical problems is that the result is independent of the coordinate system.
