Values Of Trigonometric Ratios Of Typical Angles

In trigonometry, trigonometric ratios can be derived using a triangle; more specifically, we can say that trigonometric ratios are a way to deal with the sides and angles of a right-angle triangle. Mathematically we can derive these ratios using the length of the sides of any triangle. In trigonometry, there are six types of trigonometry ratio sine, cosine, tangent, cotangent, secant, and cosecant. 

In basic studies, we find that we can derive the cotangent, secant, and cosecant using the sine, cosine, and tangent. So we can also say that sin, cos, and tan are the basic trigonometric ratios, and sec, cosec, and cost are other important trigonometric ratios. 

We mainly find the usage of this ratio to find out the ratio and length of the sides of any triangle. We can measure the values of these ratios using an acute angle; let’s take a look at the below image.

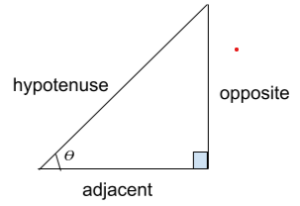
If the above-given image value of the 𝛳 is given, the ratio of any two sides of the triangle is based on the 𝛳. We can also find the value of the angle that is not given to us. We can interchange the opposite and adjacent sides of the right angle.

Different types of trigonometric ratios can be explained as follows: 

Sine or sin: This ratio can be defined as perpendicular/opposite and hypotenuse of any right-angle triangle.

Cosine or cos: This ratio can be defined as adjacent/base and hypotenuse.

Tangent or tan: This ratio can be defined as the ratio of perpendicular/opposite and adjacent/base. 

Cosecant or cosec: This ratio can be defined as hypotenuse and perpendicular/opposite

Secant or sec: This ratio can be defined as hypotenuse and adjacent/base ratio.

Cotangent or cot:  This ratio can be defined as adjacent/base and perpendicular/opposite.

We can sum up these ratios using the following tables:

Values of Trigonometric Ratios of Typical Angles 

In most of the studies, we mostly find the usage of 0°, 30°, 45°, 60°, 90° angles. We can call them typical angles, and the value of trigonometric ratios of the typical angles can be found in the following table.

Let’s try to prove some of them.

Value for 0° and 90°

Let’s consider an angle of 90° and an angle near 0°, as in the following image. 

Let the smallest angle be A then.

sinA = perpendicular/hypotenuse, 

cosA = base/hypotenuse

As we know, angle A is very small, so the perpendicular we also are very small, so the value of sinA will also be very small. We can say that it is near zero.

Also, the triangle base will be approximately similar to the hypotenuse. So the value of cosA will be approximately similar to one.

After all this, we can say that. 

sinA = 0 and cosA = 1

Now we know that 

tanA = sinA/cosA = 0/1=0

Here we have proven sin 0° = 0, cos 0° = 1, and tan0° = 0. By this, we can also say that sin 90° = 1,cos 90° = 0, and  tan 90° = not defined. 

Value for 30° and 60°

Let’s take a look at the triangle below.

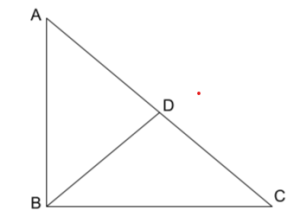
Where AC = 2BA and To get the value of 30 and 60, we prove angle C = 60 and angle A  = 30 from the above image where AD = DC = BD according to plane geometry.

Now, as we know 

sinC = BA/AC = BA/2BA = ½= sin30°

cosC = BA/AC = BA/2BA = ½ = cos60°,

Now 

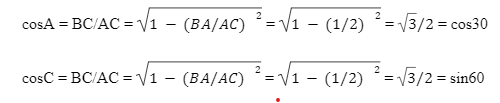
Here we can sum up the value of the trigonometric ratio for 30 and 60 in the following way:

Value for 45°

Let’s take a look at the triangle below.

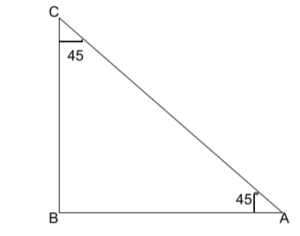
This is a right-angled triangle where the other two angles are 45°. Such a triangle will be an isosceles type of triangle.

This means AB = BC = AC/√2,

Now 

sin45 = BC/AC  = 1/√2

And 

cos 45 = AB/AC  = 1/√2

Hence proved 

Here we have seen how we can obtain the values of typical angles. To better understand the topic, let’s take a look at some of the examples/problems that can be solved using the value of the trigonometric ratio for a typical angle.

Examples

1. What is the value of cos45 sin30 + sin45 cos30?

Solution:

From the table of values of trigonometric ratio for typical angle, we can obtain the following values 

• cos45 =  sin45 = 1/√2

• sin 30 = ½

• cos 30 = √3/2

Let’s put these values in the expression.

cos45 sin30 + sin45 cos30 = 1/√2 X ½ + 1/√2 X √3/2

= 1+322

 Here the above value is our answer.

2. If,  sin60 + cos301+ cos60 + sin30= sin then,  what is the value of ?

Solution:

From the table of values of trigonometric ratio for typical angle, we can obtain the values and put them into the equation of question. As follows:

sin60 + cos301+ cos60 + sin30= 3/2 + 3/21+ 1/2 +1/2= sin

3/2 = sin

Now, we can say that.

= 60°.

Conclusion 

In this article, we have gone through the detailed introduction of the trigonometric ratios, and after that, we have discussed some of the typical angles. Along with this, we learned how to calculate the value of the trigonometric ratio of typical angles with some examples.