The circular functions are commonly known as the Trigonometric functions. It is one of the most important concepts in mathematics and physics and there are several trigonometric applications. In simple terms, the functions of trigonometry are the functions of the angles of the triangles. The relationship between the sides of the triangles and the angles of the triangles are given out by the functions of trigonometry. Therefore, there are six fundamental trigonometric functions. These functions are Cosecant, Secant, Cotangent, Tangent, Cosine, and Sine. These functions of trigonometry are commonly known as Cosec, Sec, Cot, Tan, Cos, and Sin, respectively. 

With the use of these functions of trigonometry, we can find numbers of identities and formulas which helps in denoting and pointing at the bond between the functions and the measure of the angle of a triangle. Let us look at these functions of trigonometry and identities to solve examples of trigonometry. 

Trigonometric Functions

The six fundamental functions of trigonometry are Sin, Cos, Tan, Cot, Sec, and Cosec. The primary classifications of the functions of trigonometry are- Sin, Cos, and Tan. The other three functions, that is- Cot, Sec, and Cosec can be derived from the primary classification. 

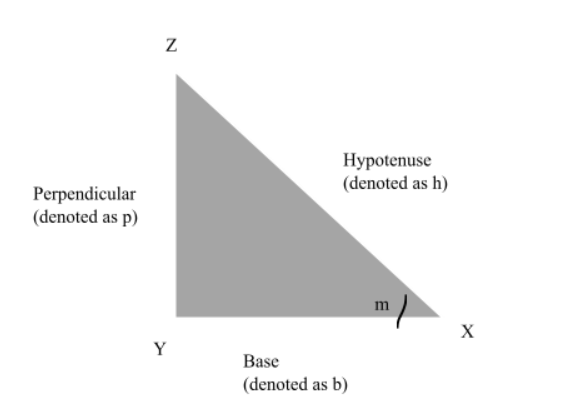
In the above diagram of the Right-angled triangle, the given elements are as follows-

  • The Perpendicular line (p) is line ZY. It must also be noted that lien ZY is right opposite to angle m.
  • The Hypotenuse (h) is line ZX. 
  • The Base (b) is line XY. The line XY is directly adjacent to angle m. 

Let us look at how the primary classifications of trigonometric functions can be derived from the above diagram.

  • Sin Function: The Sin function of an angle is said to be the ratio between the line opposite to the angle and the hypotenuse of the triangle. That is, 

Sin m = p ⁄ h = ZY ⁄ ZX

  • Cosec function: Cosec function of an angle is the reciprocal of the Sin function of an angle. That means, 

Cosec m = h ⁄ p = ZX ⁄ ZY

  • Cos Function: The Cos function of an angle is said to be the ratio between the adjacent side, that is, the base of the triangle and the hypotenuse of the triangle. That is, 

Cos m = b ⁄ h  = XY ⁄ ZX

  • Sec Function: Sec function of an angle is the reciprocal of the Cos function of trigonometry. That means, 

Sec m = h ⁄b = ZX ⁄ XY

  • Tan Function: The Tan function of an angle can be said to be the ratio between the side opposite to the angle, that is, the perpendicular line of the triangle and the adjacent side of the angle, that is, the base of the triangle. That is, 

Tan m = p ⁄ b = ZY ⁄ XY

  • Cot Function: The cot function of an angle is the reciprocal of the Tan function of trigonometry. That means, 

Cot m = b ⁄ p = XY ⁄ ZY

Important Identities and Formulas

Some of the most important identities and functions that helps to solve an example of Trigonometry are as follows-

  • Odd and Even Functions: All the functions of trigonometry, except the Cos function and the Sec functions, are odd- that is negative. 
  • Pythagoras Identity: The trigonometric functions concerning Pythagoras theorem are-  

Sin²m+Cos²m=1

1+Tan²m= Sec²m

Cosec²m = 1+Cot²m

  • Operational Identities: The operational identities are-

Sin(m + n) = Sin(m) . Cos(n) + Cos(m) . Sin(n)

Cos(m + n) = Cos(m) . Cos(n) – Sin(m) . Sin(n)

Tan(m + n) =   tan(m) + tan(n) ⁄ 1- tan(m) . tan(n)

Tan(m – n) = tan(m) – tan(n) ⁄ 1+ tan(m) . tan(n)

Cos(m – n) = Cos(m) . Cos(n) + Sin(m) . Sin(n)

Sin(m – n) = Sin(m) . Cos(n) – Cos(m) . Sin(n)

These identities can be used for several purposes. 

Conclusion

The circular functions are commonly known as the Trigonometric functions. the functions of trigonometry are the functions of the angles of the triangles. The relationship between the sides of the triangles and the angles of the triangles are given out by the functions of trigonometry. These functions are Cosecant, Secant, Cotangent, Tangent, Cosine, and Sine. The most commonly used functions of trigonometry are the primary function of trigonometry- Sin, Cos, and Tan. The Cot, Sec, and Cosec functions are the reciprocal of the primary functions.