Types of Matrices

Matrices are the plural of a matrix which is an array of numbers. There are various types of matrices, and they are divided and categorised based on the different values of elements. In this article, we will discuss every type of matrix with examples.

Types of Matrices

Column Matrix

The matrix which has only one column is known as a column matrix. So A= [aij]mxn if n=1 and hence the value of the column matrix would be 1.

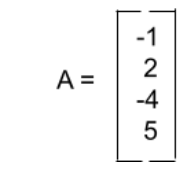
One example of a column matrix is

It is a column matrix of 4×1.

Another example can be 

P=

Where P is in a 3×1 order matrix.

Row Matrix

A matrix that consists of only one row is known as a row matrix. So, if A = [aij]mxn is a row matrix if m=1. Hence a row matrix can be represented via A= [aij]1xn

It is called a row matrix as there is only one row, and hence the order of the row matrix will be 1xn.

Let us take an example

A= [2,3,4,6] is a row matrix of order 1×4.

Vertical Matrix

A vertical matrix is in the order of m x n where m>n.

An example is 

Singleton Matrix

A matrix where there is only one element is referred to as a singleton matrix. So A= [aij]mxn if m=n=1 

For e.g., [2], [3], [b] ,[] are some of the singleton matrices

Horizontal Matrix

It is a type of matrix that is in order m x n and n>m

Let us take an example 

In this m=2 and n=4.

Null or Zero Matrix

In a matrix, when all the elements are zero, they are called a zero or null matrix since it is generally denoted by 0.

So, A= [aij]mxn if aij =0 for all i and j.

Let us take an example,

A= where this is a 3×2 null or zero matrix

Square Matrix

A square matrix is a type of matrix where the number of rows and the number of columns are equal.

So, A= [aij]mxn if m=n 

Let us take an example

It is a square matrix of order 3 x 3. 

Diagonal Matrix

In a diagonal matrix, all the elements in a square matrix except the principal diagonal are zero.

So, a square matrix A= [aij] becomes a diagonal matrix when aij = o and when i ≠ j

Example

It is a diagonal matrix of the order 3 x 3 and denoted by a diagonal [2 3 4]. The important thing is that all elements are zero except for the diagonal elements. Hence two things can be said with certainty.

1. A diagonal matrix will always be a square matrix.

2. In a diagonal matrix, all the diagonal elements are characterised in a general form where aij where i=j.

Hence the matrix will have one diagonal.

Scalar Matrix

A scalar matrix is when every element in the diagonal of a diagonal matrix are equal. It is known as a scalar matrix. 

Hence a square matrix is when A= [aij] is a scalar matrix

when Aij= when k is a constant

So let us take an example

It is a scalar matrix.

Identity Matrix

When all the elements in a principal diagonal in a diagonal matrix = 1. It is called a unit matrix and is also known as an identity matrix. So, A= [aij] becomes an identity matrix when 

I3 =

Hence, we can conclude the following points

1. Every  identity matrix is a scalar matrix.

2. Every scalar matrix is a diagonal matrix.

3. Every diagonal matrix is a square matrix.

Note: The reverse of any of the cases listed above is not valid.

Equal Matrix

Equal matrices are matrices that are equal in terms of their elements.

Conditions

Matrices A and B are equal if they are in the same order and their corresponding elements are equal. 

So, Two Matrices

A= [aij]mxn and B=[bij] r x s will be equal when,

1. m=r, i.e., the number of the rows in A and B will be equal

2. n=s, i.e., when the number of columns in A and B will be equal

3. aij = bij where i= 1,2 and j=1,2 and their elements are equal

These are equal matrices as 

a1 = 1, while a2 = 6, and a3 = 3

 b1 = 5,  while b2 = 2, and b3 = 1.

Triangular Matrix

A square matrix is considered triangular when all the elements above the principal diagonal else below the principal diagonal are zero.

There are principally two types.

Upper Triangular Matrix

A square matrix [aij ] is known as an upper triangular matrix where if aij = 0 when i>j

It is an upper triangular matrix of order 3 x 3

Lower Triangular Matrix

A square matrix [aij ] is known as a lower triangular matrix where if ij = 0 where i

It is a lower triangular matrix of order 3 x3 

Singular Matrix and Non-Singular Matrix

A matrix is a singular matrix when the determinant |A|= 0. For a non-singular matrix, the determinant |A|≠ 0.

Symmetric and Skew Symmetric Matrices

A symmetric matrix is a square matrix where aij = aji for all values of i,j

Let us take an example.

This is symmetric as a12 = 2= a21 a31= 3= a13

A is symmetric if A’=A where ‘A’ is the transpose of a matrix

Skew Symmetric Matrix is a square matrix. For example, A=[aij] is a skew-symmetric matrix where aij = aji for all values of i,j

[putting j=i] aii =0

Thus, in skew-symmetric matrices, all diagonal elements are zero.

A= B=

These are skew-symmetric matrices.

Always remember, a square matrix A is also a skew-symmetric matrix if A’ = – A

Conclusion

These are some of the types of matrices, and we hope that you get a fundamental understanding through them. These types of matrices are essential to understand, especially regarding understanding the operation of the matrices.