Trigonometry-Identities & Equations-Trigonometric Ratios of Allied Angles

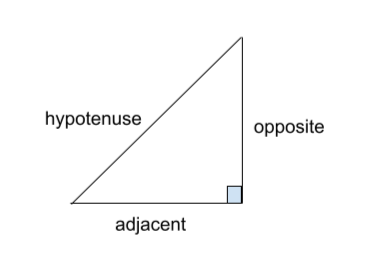
In a right-angle triangle, sides with 90° angles are called opposite and adjacent sides, and the biggest side in front of 90° is called the hypotenuse. Using these sides of a right-angle triangle, we can obtain trigonometric ratios. Let’s take a look at the below table.

Here we can see that the trigonometric ratios are the ratio of these sides. The above table represents the ratio that can be given for an angle.

Two angles can be considered allied angles only if the sum or difference of these angles is either 0°, 90°, or multiple of 90°. For example, 120° and 30° are allied angles because their difference is 90°. 

Using the above points, we can say six trigonometric ratios sine, cosine, tangent, cotangent, cosecant, and secant. And when the two angles represent either 0°, 90°, or multiple of 90° in their addition or subtraction can be called allied angles. This article is focused on explaining trigonometric ratios of allied angles. 

Talking about the formula of trigonometric ratios of allied angles, some of the basic examples are as follows:

sin(-θ°) = -sinθ°

We can extract these formulas using the following table:

It is very simple to extract the formula; for example, if α = 90 – θ, then 

Sinα = sin(90 – θ) = cosθ.

                              = sin(90 – θ) = cosθ.      ………(1)

Equation one is an example of the formula of the trigonometric ratio of allied angles. Some of the most used formulas are listed below.

• sin(90 – θ) = cosθ
• cos(90 – θ) = sinθ
• tan(90 – θ) = cotθ
• sin(90 + θ) = cosθ
• cos(90 + θ) = -sinθ
• tan(90 + θ) = -cotθ

In the above section, we have seen the explanation of trigonometric ratios and allied angles; along with that, we discussed trigonometric ratios for allied angles. We can use these formulas in a variety of complex trigonometric problems to make the problem easily solvable. To understand their working, we are required to solve some of the problems using the trigonometric ratios of allied angles. Let’s move towards the examples.

Trigonometric Ratios of Allied Angles

This section includes some of the conditions in trigonometry, where using the trigonometric ratio of allied angles can make the problem easy or solved.   

1. Problem: What is the value of sin 150°?

Solution:

In this problem, we have an angle of 150°. that can also be written as-

150° = 90° + 60°

Now let’s put this in sin function:

Sin150° = sin(90° + 60°)

From the above table, we can find that: 

sin(90 – θ) = cosθ

We can compare θ of the formula with 60°, then 

sin(90° + 60°) = cos 60°.

We can find the value of trigonometric ratios in the below table.

From the above table,

Cos 60 = ½.

So we can say that 

Sin150° = ½.

Let’s move toward the next problem.

• Problem: what is the value of cos(-210°)?

Solution:

In this problem, we have an angle of -210°. We can write it as follows:

-210° = -(180 +30)°

Now cos(-210°) can be written as

cos(-210) = cos[-(180 + 30)]

We also know from the table,

cos(-θ) = cosθ

So 

cos[-(180 + 30)] = cos(180 + 30)    

 Also, from the above table 

cos(180 + θ) = -cosθ

So 

cos(180 + 30) = cos 30

From the table of trigonometric ratios, we find cos 30 = √3/2,

So 

cos(-210) = √3/2.

Let’s move toward the next problem.

• Problem: What is the value of tan(-1215°)? 

Solution :

We can write tan(-θ) = -tanθ

So 

tan(-1215°) = -tan(1215).

Now 1215 can also be written as 

1215 = 3 X 360 + 135

So 

-tan(1215) = tan(3 X 360 + 135)

From the table, we can write

 tan(nℼ + θ) = tanθ

So 

-tan(1215) = -tan(135𝆩)

Also 

135 = 90 + 45

So 

-tan(135) = -tan(90 + 45)

From the table, we can find that 

tan(90 + θ) = -cotθ

So 

 -tan(90 + 45) = cot(45)

From the table of trigonometric ratios, we find cot45 = 1

So 

tan(-1215) = 1.

Here we have seen some examples related to the trigonometric ratio of allied angles.

Conclusion 

In the article, we have gone through the trigonometric ratios and allied values. We have also seen some examples of trigonometric ratios of allied values and solved some of the problems to find our value of allied angles using the trigonometric ratio.