Trigonometry-Identities & Equations-Trigonomertic Ratios Of Multiple And Sub-Multiple Angles

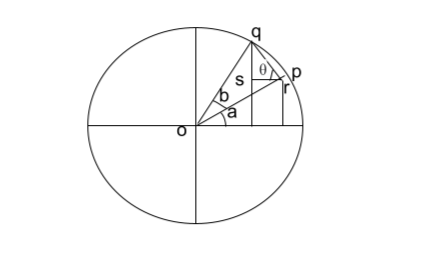
From the above circle, we can say that.

sin(a+b) = qu

                            = qs+su

                           =qs+rt

                                         =qr sin+or sin a

Also,

qr=sin b, θ = 90-a, or= cos b

Let’s put the above values in the main equation, 

sin(a + b) = sin b sin(90-a)+cos b sin a

=sin a cos b + cos a sin b

Similarly, we can prove the relation. 

sin(a-b)= sin a cos b-cos a sin b

Let’s move toward the next property.

cos(ab)= cos a cos b sin a sin b

Let’s refer to the above image, from which we can say that.

cos(a+b) = ou

= ot – tu

= or cos a-pq cos θ

= cos a cos b-sin a sin b

Similarly, we can prove that.

cos(a-b) = cos a cos b + sin a sin b

Let’s move toward our next property.

tan(a b) = (tan a tan b)/1tan a tan b

As we know tanA = sinA/cosA then 

tan(a+b) = sin(a+b)/cos(a+b)

= (sin a cos b + cos a sin b)/(cos a cos b – sin a sin b)

In the above equation, dividing the numerator and denominator by cosacosb can give us our required relation.

The above-given properties are very few but one of the most important and used properties of multiple and submultiple angles. After understanding them, we are ready to move toward the ratios of multiple and submultiple angles.

We mainly find the usage of the angle ratio in terms of half value of angle and one-third value of the angle. To generate the intuition behind the topic, we will look at the ratio of these two only.

Ratio angle in terms of the angle divided by two.

• sina=sin(2a/2)=2sina/2cosa/2
•  
• sina=2sin(a/2)cos(a/2) =2sin(a/2)cos(a/2)cos2(a/2)+sin2(a/2) = 2tan(a/2)1+tan2(a/2)   
•  
• sina =2tan(a/2)1+tan2(a/2) = (2/cot(a/2))1+cot2(a/2) =2cot(a/2)1+cot2(a/2)  
• cosa = cos(2a/2) = cos2(a/2) – sin2(a/2)  = 1-sin2(a/2) -sin2(a/2)=1-2sin2(a/2)
  •  
• cosa=cos2(a/2) – sin2(a/2)  = cos2(a/2) – 1 +cos2(a/2) = 2cos2(a/2) – 1
  •  
• cosa = cos2(a/2) – sin2(a/2)=cos2(a/2) – sin2(a/2)cos2(a/2) + sin2(a/2) = 1-tan2(a/2)1+tan2(a/2)=cot2(a/2) – 1cot2(a/2) + 1
  •  
• tana=2tan(a/2)1-tan2(a/2)=2cot(a/2)cot2(a/2)-1
  •  
• tana=cot2(a/2)-12cot(a/2)= 1-tan2(a/2)2tan(a/2)

Ratio angle in terms of the angle divided by three.

• sina= sin(3a/3)=3cos(a/3)-4cos3(a/3)

• cosa=cos(3a/3)=3cos(a/3)-4coss3(a/3)

• tana=tan(3a/3)=3tan(a/3)-tan3(a/3)1-3tan2(a/3)

  Here we have gone through some important ratios of multiple and submultiple angles. We many journals, we may find confusion about multiple angles; for example, in some places, we find an example of angles in the multiplication of 2, 3, or 4, and they call it multiple angles such as 2a, 3a, 4a are an example of multiple angles and a/2, a/3 and a/4 are an example of submultiple angles.

Formulas

In this article, we are going to take a look at some of the important formula we find for trigonometric ratio of submultiple and multiple of an angle:

1. | sin A/2 + cos A/2 | = √(1 + sin A)  
2. sin A/2 + cos A/2 =  + √(1 + sin A), if 2nπ – π/4 ≤ A/2 ≤ 2nπ + 3π/4
3. | sin A/2 – cos A/2 | = √(1 – sin A)
4. a cos A + b sin A < √a2 + b2
5. tan A/2 = ± √(1-cos A) / (1+cos A)

In the above-given formulas, we can easily replace the values of sub-multiple angles with multiple angles and make them work in either of the conditions. 

Let us make our understanding clearer about the topic by solving an example. Here to understand it more, we can find the value of cos 67 1°/2. 

Consider, a = 67.5°

Using the above equations, we know that. 

  cosa= 2cos2(a/2) – 1

So,

cos2a=2cos2a – 1

Here, we also know that cos(135) = -1/√2, so,

-1√2=2cos2(67.5) – 1

2cos2(67.5) = 1-12

We can also write it as, 

cos2(67.5) = 2-224

Now 

cos(67.5) = (2-222

Here we have seen how we found the value of cos(67.5) using the ratio of multiple and sub-multiple angles.

Conclusion 

In the article, we have discussed the trigonometric ratio of multiple and submultiple angles. With this understanding, we also discussed the properties of multiple and submultiple angles. With some of the important formulas, we also discussed an example of using a ratio of multiple angles.