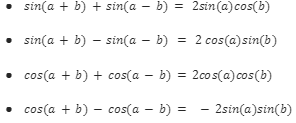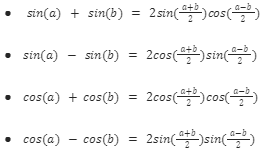Trigonometry-Identities & Equations-Transformation Formula

Transformation formula

In mathematics, trigonometric functions like sin, cos, and tan transform angles into a numerical format or vice versa; for example, sin(90) can be expressed as one and sin-1(1) can be expressed as 900. This function helps in solving a variety of mathematical expressions and problems. With this feature, they also include mathematical features with them. Transformation is one of the important features of these trigonometric functions that can transform trigonometric equations. We can transform the sum or difference of the trigonometric ratios of the compound angles into products of the trigonometric ratios of the angles or vice versa. 

Involving these features into account, we can resolve various geometrical and trigonometric problems with them. In many places, we can find difficulties in obtaining results using the sum of the angles whereby transforming them into products can make obtaining required results easy. By the above points, we can say that we are required to have the same formula that can be called transformation formulas in trigonometry for the transformation of trigonometric functions. We can categorise these formulas into two categories. 

• Formulas for transforming sum or difference into products   
• Formulas for transforming the product into sum or difference

Let’s take a look at these formulas one by one. 

Formulas for transforming sum or difference into products  

We will start by looking at those formulas that can help us transform the sum or difference of trigonometric functions into products of trigonometric functions. 

Let’s say we have two angles a and b. As we know that

1. sin(a+b) = sin(a)cos(b)+cos(a)sin(b)
2. sin(a-b) = sin(a)cos(b)- cos(a)sin(b)

Let’s add these above equations. 

sin(a+b)+sin(a-b)= 2sin(a)cos(b)

The above-derived equation is a transformation formula for the difference of angles. 

If we subtract this equation, we get  

sin(a+b)-sin(a-b)= 2 cos(a)sin(b)

This above derived equation is a transformation formula for difference for difference of angles. 

some of the transformation formulas of this categories are as following:

• sin(a+b)+sin(a-b)= 2sin(a)cos(b)
• sin(a+b)-sin(a-b) = 2 cos(a)sin(b)
• cos(a+b)+cos(a-b)=2cos(a)cos(b)
• cos(a+b)-cos(a-b)= -2sin(a)sin(b) 

We can use the following way for remembering the above-given formulae.

Here in the above, we have seen some of the formulas for transforming the sum or difference of the formula into products with the procedure using which we can derive them. Let’s take a look at the formula that can transform products of the angles into sum or difference of the angle,

Formulas for transforming the product into sum or difference

In the above, we have seen how we derived a transformation formula using the formulas of sine trigonometric function. For this section, we will use the formula of the cosine trigonometric function.

As we know,

• cos(a)cos(b)-sin(a)sin(b) = cos(a+b)
• cos(a)cos(b)+sin(a)sin(b) = cos(a-b)

Let’s add them 

2cos(a)cos(b) = cos(a + b) + cos(a -b)

Here we get the value of the product transferred into the sum. In most cases, we find the representation of these formulas in the following way.

Here we have seen the transformation formulas and their types with some of the examples of them. To create a better understanding, we must go through some of the examples using these formulas.

Example 

Let’s take a look at the below trigonometric expression.

2sin2𝛳cos𝛳

By looking at the equation, we can say this is a product function of trigonometry.

Now using the formula, 

2sin(a)cos(b)=sin(a+b)+sin(a-b)

We can transform our equation into a sum or difference equation.

2sin2𝛳cos𝛳 = sin(2𝛳+𝛳) + sin(2𝛳-𝛳) 

                     =sin(3𝛳)+sin(𝛳)

We have seen an example of product transformation into a sum or difference in the above. 

Let’s take a look at the below equation.

cos2𝛳- cos6𝛳

This equation is a sum function of trigonometry.

We can rewrite this equation as follows

cos2𝛳- cos6𝛳= cos(4𝛳-2𝛳) – cos(4𝛳+2𝛳)

The right hand side equation can be compared to the formula,

So, we can also rewrite our equation as follows

Here in the above, we have transformed an equation with the difference of trigonometric function into the product of trigonometric function.

Conclusion 

In the article, we have discussed the transformation in trigonometry and see the transformation formulas and their type with some of the examples of transformation formulas. We have also gone through some of the examples of transformation using the transformation formula of trigonometry. 

We can rewrite this equation as follows

cos2𝛳- cos6𝛳= cos(4𝛳-2𝛳) – cos(4𝛳+2𝛳)

The right hand side equation can be compared to the formula,