Trigonometry can be used to understand the relationship between object heights and distances. Trigonometric formulas can be used to calculate the height and distance of anything. If you know the distance between you and the building and the angle at which you can see the top of the building, you can calculate its height. We use trigonometry to calculate the height because the ground surface, the building’s height, and the line of elevation all form a right-angle triangle with 90 degrees between the building and the ground.
It is a useful application of trigonometry that allows us to calculate the height and distance of any object from any place that is not directly observable. If you know the angle of elevation/depression from a given place.
Below are the few terms that are important to know for a better understanding of heights and distances:
- Line of Sight: The line drawn from an observer’s eye to a point in the object viewed by the spectator is known as the line of sight.
- The angle of elevation: The elevation angle is the angle formed between the horizontal and the line of sight that connects an observation point to an elevated object.
Consider a circumstance in which a person is standing on the ground and looking up at an item that is at a certain height, such as the roof of a building. The line of sight is the line that connects a person’s eye to the top of a building. The angle of elevation is the angle formed by the line of sight and the horizontal line.
- The angle of depression: The depression angle is the angle formed by the horizontal and line of sight from an observation point to an item below the horizontal level.
Consider another scenario in which the person is standing at a certain height with the object he is viewing. In this scenario, the line of sight is the line that connects the man’s eye to the bottom of the building. The angle of depression is the angle formed by the line of sight and the horizontal line.
Before comprehending the height and distance calculation, you must first understand the concepts of height and distance.
Height – Height refers to the measurement of an item in the vertical direction.
Distance – The measurement of an item in the horizontal direction from a specific point is known as distance.
The height of an object is calculated by measuring its distance from the object. When estimating the height of an item, the angle of elevation at the top is taken into account. The height of the object divided by the distance from the object is called the tangent of the angle.
Trigonometric Ratios:
Trigonometric ratios are used to address height and distance problems. We know that the angle’s trigonometric ratio determines the relationship between any two triangle sides. Let’s take a closer look at each of the trigonometric ratios.
Let us suppose there is a right-angled triangle ABC, where AB is the height; BC is the distance and AC is the hypotenuse.
Therefore,
Sin θ = AB/AC
Cos θ = BC/AC
Tan θ = AB/BC
Cosec θ = AC/AB
Sec θ = AC/BC
Cot θ = BC/AB
Heights and Distances Formulas:
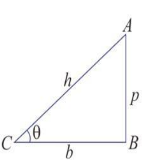
- Formula 1- In a right triangle ABC,
Sin θ = p/h ;
Cos θ = b/h ;
Tan θ = p/h
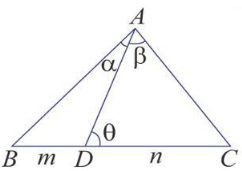
- Formula 2- In triangle ABC, if BD:DC = m:n and ∠BAD =α, ∠CAD = β and ∠ADC = θ, then (m + n) cot θ = m cot α – n cot β
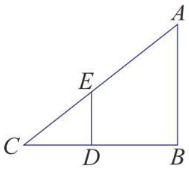
- Formula 3- In a triangle, ABC, if DE || BA, then according to the basic proportionality theorem, BD/DC = AE/EC.
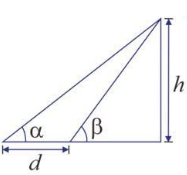
Formula 4 – The angles of elevations of two objects are α, β respectively, and the distance between two objects is d, then d=h(cot α–cot β)
Important terms :
- If the observer’s height is unknown in a problem involving heights and distances, the observer is represented by a point.
- A line segment represents the height of objects such as towers, skyscrapers, celestial bodies, and so on.
- The angle of elevation rises as the observer draws closer to the object.
- The angle of depression reduces as the observer walks away from the item.
- As a result, the angle of elevation and the angle of depression is equal.
- A decrease in the length of an object’s shadow occurs when the sun’s angle of elevation increases.
- An increase in the length of an object’s shadow is caused by a reduction in the sun’s angle of elevation.
- The term “angle of elevation” refers to an object’s position to the observer’s position.
- The angle of depression indicates that an object is moving downwards from the observer’s position.
Conclusion:
Heights and Distances is a Trigonometry application that aids in the solution of some difficult real-life situations such as determining the distance between two or more objects, mountain heights, and heavenly object distances, among others. It can also be used to determine the angle formed by an object at a given position without having to know the object’s height or distance.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out