Profile
Settings
Refer your friends
Sign out
Trigonometry is mainly focused on a different function of various angles and their evaluation. There are mainly 6 functions of an angle that are mostly used in trigonometry, and their names are Sine (sin), Cosine (cos), Tangent (tan), Cotangent (cot), Secant (sec), Cosecant (CSC). These functions help us in finding out the angles and distances which are not known from the known angles in the figures.
Trigonometry angles refer to all those angles that are provided by the ratio of the trigonometric function. It focuses on the study of the relationship between angle and side of the triangle. In this, the angle is from 0° to 360°. The mainly used angles are 0°, 30°, 45°, 60°, 90°, 180°, 270°, 360°. The angles that are mainly used are 0°, 30°,45°,60°,90°. These are different angles of different functions and each of them carries different values.
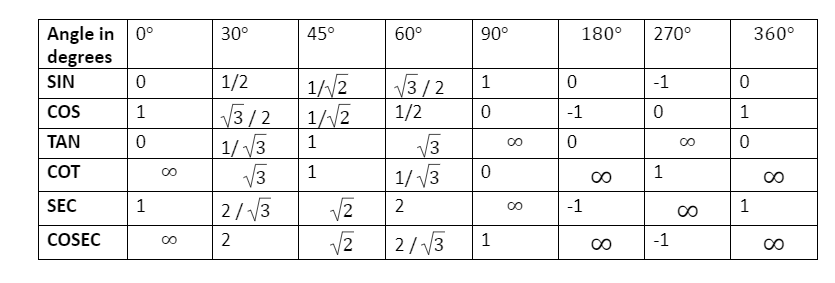
TRIGONOMETRICAL TABLE:
The table is given below here which gives us all the information of the values of every angle relating to its function:
TYPES OF ANGLES:
COMPLEMENTARY ANGLE:
When adding 2 angles, the result comes 90 degrees then the angle comes to be known as the complementary angle. E.g. if the 1st angle is x and another angle is 90°– x. so if we use that in trigonometry ratios then:
- Sin (90°-A) = cos A and cos (90°-A) = sin A.
- Tan (90°– A) = cot A and cot (90° – A) = tan A.
- Sec (90° – A) = cosec A and cosec (90°-A) = sec A.
so thus we can conclude that the angles change when they complement each other.
Let’s take an example:
To find the complement of 2 x + 52°, subtract the angle from 90°.
So, therefore,
90° – (2 x + 52°) = 90–2 x–52
= 38° – 2 x.
So the complement of 2 x + 52° is 38°– 2 x.
SUPPLEMENTARY ANGLE:
When the addition of 2 angles equals 180 degrees, then the angle is known as supplementary angle. E.g. if the 1st angle is x, then the other angle will be 180°–x. If we use that in trigonometric ratios, then:
- Sin (180°–A) = sin A.
- Cos (180° – A) = cos A.
- Tan (180° – A) = tan A.
TRIGONOMETRY FORMULAS:
SUPPLEMENTARY FORMULA:
Let’s assume sum as . So the formulas are:
- Sin (π – α)= sin α.
- Cos (π – α) = – cos .
- Tan (π – α) = – tan .
- Cot (π – α) = – cot .
ANTI SUPPLEMENTARY ANGLE:
Let’s assume difference as (π)
- Sin (π + α) =–sin α
- Cos ( π + α ) = – cos α
- Tan ( π + α ) = tan α
- Cot (π + α ) = cot α
OPPOSITE ANGLES:
Let’s assume sum as 2π
- Sin (2 π–α) =–sin α
- Cos (2 π – α ) = cos α
- Tan (2 π – α ) = -tan α
- Cot (2 π–α) =–cot α
COMPLEMENTARY ANGLE:
Let’s assume sum as (π/2)
- Sin ( π / 2 – α ) = cos α.
- Cos (π / 2 – α ) = sin α.
- Tan (π / 2–α) = cot α.
- Cot (π / 2–α) = tan α
CONCLUSION:
As we have realized, the importance is trigonometry and how it can be used in many areas like architecture, astronomy. E.g. without even climbing up the tree, we can easily find out the height of the tree. We can get to the conclusion that life would be tougher without trigonometry, so thus trigonometry was a wonderful invention, and it helps many architects in evaluating many things without even getting into them. So it helps us in real life too apart from exams or tests in the exam. Without trigonometric angles, bringing out value is impossible because it gives them the values which help in solving many problems.
