The Triangle is one of the crucial aspects of mathematics. The modern expression of the triangle can be well referenced from the Latin word “triangulus” or “three-cornered”. They also constitute the pillars of geometry, trigonometry, Euclid’s laws, and various other components of Mathematics.
What is a triangle?
Triangles are a type of polygon having three sides and three angles or vertices that depend on the type of the polygon. Each triangle fundamentally consists of three edges, three angles and all of the edges intersecting each other at three vertices. The triangle is a two-dimensional geometrical figure responding to the Euclidean plane. Triangles are vital for mathematical study and triangle type use and applications have developed further.
Properties of Triangles
The interesting properties of triangles and their types helps us the relationship between different sides and angles. These crucial elements of triangles also help us understand the association of triangular properties and types of the triangle with other aspects of geometry and understand connections with other mathematical components.
Angle Sum Property
The sum of all the interior angles of a triangle is not more than 180 degrees. This property of a triangle helps us simply understand the essentials of drawing a triangle, identifying the basic angle sum property helps us also use its application on finding the edges of a triangle, for example, the three angles of a triangle are P, Q and R then the property follows that: ∠P + ∠Q + ∠R= 180°.
Triangle Inequality Property
As per the triangle inequality theorem, the cumulative of the measurements of any two edges of a triangular polygon is more than the measurement of the final side. Hence, if we consider a triangle having sides namely a, b and c with measurements of four units, six units, and three units respectively.
Hence the triangle ABC would provide us with the following conclusions:
- a + b > c (4+6 > 3)
- b + c > a (6+3 > 4)
- a + c > b (4+3 > 6)
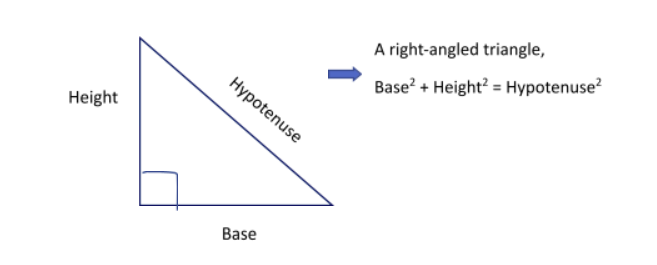
The Pythagoras property
The most vital fact to apply this property is to understand that this property is only applicable for right-angle triangles i.e., the triangles having one of the vertices bearing an angle of 90 degrees. Also, the underlying side of the right angle is termed as a base and the associating side of the right angle is termed as height. Hence the conclusion of this property gives us an equation of Pythagoras theorem as Base² + Height² = Hypotenuse². This property also divides the right-angle triangle into a specific triangle type.
Exterior Angle property
The property says that the sum of the opposite interior angles is equal to the exterior angle of the corresponding part of the considered interior angle. Further to also be aware of the fact that the sum of the exterior angles of each interior angle is always equal to 360 degrees. Both the exterior angle and Pythagoras property also helps distinct types of triangles.
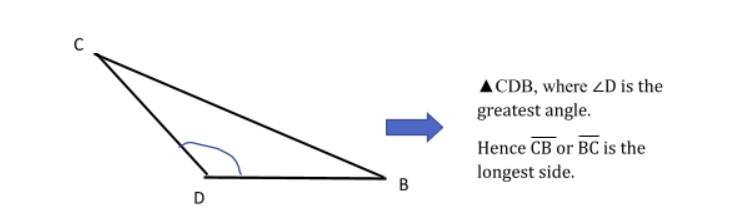
The side opposite the greater angle is the longest
Assuming a triangle CDB in which angle D is the greatest angle among the other than the side opposite to the angle will be side BC or CB. Hence the side CB can also be termed as the longest side.
Other properties
- Area of a right-angled triangle: To find the area of a right-angled triangle that is one of the angles being 90 degrees then the formula area= 1/2 * base * height is used.
- The perimeter of a triangle: This property is used to determine the total boundary length of the triangle. The procedure used involves the sum of the length of the edges or sides of the polygon.
- Heron’s Formula: This property helps us to determine the area or the space occupied inside any type of triangle. This triangular property proceeds in the formula of A = √s(s−a) (s−b) (s−c), where A is the area and “s” is the semi perimeter that can be found by s= (a+b+c)/2.
Types of triangles
Triangles can be classified into various triangle types based on their angles and sides. The classification of types of triangles helps us identify and get well briefed about the vivid applications and their roles in further geometric and mathematical applications.
Based on interior angles, the types of triangles are:
- Acute Angle: If all the interior angles of a triangle are less than 90 degrees then the triangle is an acute-angled polygon.
- Obtuse Angle: If any of the interior angles of a triangle is greater than 90 degrees.
- Right Angled Triangle: If any of the angles of a triangle is equal to 90 degrees.
Based on the sides of the triangles the types of triangles are:
- Equilateral triangle: The triangle has three equal sides and three equal angles in which each of the interior angles is equal to 60 degrees.
- Isosceles triangle: The triangle in which any two sides and inside angles are equal is called the isosceles triangle.
- Scalene triangle: This triangle type that does not have any two sides or angles that are equal is called the scalene triangle.
Conclusion
The uses and insights of triangular properties and types of triangles can be ranging from ancient pyramids to modern-day bridges, architectures, and developing the fields of mathematical and geometrical knowledge. The article mainly focuses on helping us understand the vivid triangular properties and triangle types, also trying to clear additional queries through the frequently asked questions segment.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






