Introduction

This easy-to-understand and well-written article aim to help grasp the concepts of analytical geometry, the three dimensions (or 3D) in analytical geometry, and the three dimensions – various forms of eq. of line.

To represent or find the equation in any line or 3D space, the knowledge of 3D coordinates (or analytical) geometry is required.

The vector and cartesian forms make up the three dimensions – various forms of eq. of line.

The equation of a line in –

Vector form:    r->= a-> + λ d->  and r->= a->+ λ (b-> – a->)

 Cartesian form: 

(x – x1) / (x2 – x1) = (y – y1) / (y2 – y1) = (z – z1) / (z2 – z1), and 

(x – x1) / a = (y – y1) / b = (z – z1) / c.

Introduction to the Concept of Analytical Geometry

• Analytical geometry is the field of mathematics that uses algebraic symbols and methods to represent and solve an equation for a problem in geometry.
• Analytical geometry is commonly known as coordinate geometry and sometimes as cartesian geometry.
• Analytical geometry is the study of geometry by the use of a coordinate system.
• Applications of analytical geometry: 

• Its concept is used in the field of physics, engineering, aviation, rocketry, space science, and spaceflight. 
• It provides the foundation for most modern geometrical fields, such as algebraic geometry, differential geometry, discrete geometry, and computational geometry.
• Analytical geometry establishes the correspondence between geometric curves and algebraic equations, making it possible to reformulate problems in geometry in terms of equivalent problems in algebra and vice versa.

Introduction to the concept of Three-Dimensional Coordinate System

• To represent (or locate) any point or object in space, the knowledge of 3D coordinate (or analytical geometry) is required.
• In the three-dimensional coordinate system, the coordinates of a point A are represented as A (x, y, z). The point exists in an XYZ plane, where x, y, and z represent the distance of point A from the origin in X, Y, and Z coordinate axes, respectively.
• The coordinates of the origin in the 3D coordinate system are O (0, 0, 0).
• The x, y, and z axes divide the XYZ plane into eight equal parts. Each part is known as an octant.

Introduction to the concept of Three Dimensions – Various Forms of Eq. of Line

• In three-dimensional space, the equation of a line can be obtained if we know the coordinates of a point that the line passes through as well as the direction vector of the given line, which represents the direction of the given line.
• The vector and cartesian forms make up the three dimensions – various forms of eq. of line.

Vector Form

There are two cases of representing the equation of a line in vector form.

1.  r = a-> + λ d->  
2.  r =  a-> + λ (b-> – a->)

Case 1 is the equation of a line passing through a point whose position vector is   a-> and parallel to  d->.

Case 2 is the equation of a line passing through two points whose position vectors are a-> and  b->, respectively.

Cartesian Form

• There are two cases of representing the equation of a line in cartesian form.

1. (x – x1) / (x2 – x1) = (y – y1) / (y2 – y1) = (z – z1) / (z2 – z1). 
2. (x – x1)/a = (y – y1)/b = (z – z1)/c

Case 1 is the equation of a line passing through two points whose coordinates are (x1, y1, z1) and (x2, y2, z2). It is also the standard equation of a line in three-dimensional space.

Case 2 is the equation of a line parallel to the vector a î + b ĵ + c kˆ, and passing through a point whose coordinates are (x1, y1, z1). 

• Proof of case 2 of the cartesian form.

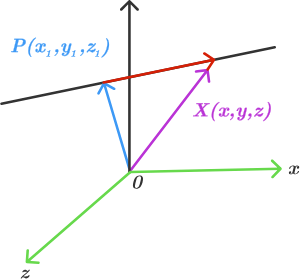
Considering a line that passes through the point P (x1, y1, z1) and whose direction vector is  d->= (a, b, c).

Here, a, b, and c are non-zero real numbers.

Assuming A = (x, y, z) as a random point on the given line.

Consider the figure below:

From the figure, we can see that the arrow represents the vector P->X and is parallel to the vector d->.

We can write,

P->X = t d->.

• [(x – x1), (y – y1), (z – z1)] = t . (a, b, c)
• t = (x – x1)/a = (y – y1)/b = (z – z1)/c

Hence, we can conclude that any point A = (x, y, z) on the line will satisfy the following equation:

(x – x1)/a = (y – y1)/b = (z – z1)/c.

Conclusion 

Through this article, we have understood and grasped the concepts of analytical geometry, three dimensions (or 3D) in analytical geometry, and three dimensions – various forms of eq. of line in analytical geometry.

In the three-dimensional coordinate system, the coordinates of point A are represented as A (x, y, z), and the vector form and cartesian form make up the three dimensions – various forms of eq. of line.

They now know that (x – x1) / (x2 – x1) = (y – y1) / (y2 – y1) = (z – z1) / (z2 – z1) is the standard equation of a line in three-dimensional space.