Three Dimensions-Direction Cosines And Ratios

Introduction

Analytical geometry deals with the geometrical figures in the coordinate system. In three-dimensional geometry, direction ratios and cosines define some critical properties of the lines or vectors. Direction cosine and ratios come into existence as soon as a vector comes into existence in a three-dimensional coordinate space. The direction cosines are cosines of the angle that the vector makes with the positive coordinate axes of the three-dimensional euclidean space. 

Three positive coordinate axes make three direction cosines for each vector. The proportional numbers to direction cosines of a vector are its direction ratios. 

Components of a vector on a straight line

The component of a vector on a straight line is the length of the line segment that the vector creates on the considered line if perpendiculars are dropped from its endpoint to the considered line.

Suppose there is a vector v, then, its component on a straight line L is given as:

v cos (where  is the angle between that vector in consideration and line L., and  ||v||  is the magnitude of that vector)

This component is a scalar quantity. 

Direction cosines of a vector

The direction cosines are cosines of the angle that the vector makes with the positive coordinate axes of the three-dimensional euclidean space. 

Suppose there is a vector v, in three-dimensional Euclidean space R3 

Then the direction cosines of that vector, is the component of the unit vector in the direction of v to the positive coordinate axes.

For considered vector, the unit vector in its direction is obtained as

u = v/||v||

Where ||v|| is the magnitude of that vector. (we kept the direction, but scaled the size of the vector to unit size).

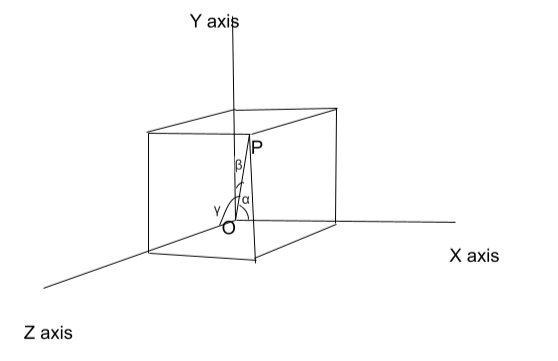
Assuming the angles made by the vector with the positive coordinate axes are:

• Angle between v and x-axis be α
• Angle between v and y-axis β
• Angle between v and z-axis be  γ

Then, the direction ratios are defined as:

cos(α), cos(β), cos(γ)

They are usually written l, m, and n

Finding the direction cosines of a vector

Suppose that the considered vector is v = 3i + 4j + 12k

Then, the unit vector for this vector is:

u = v/||v||

u = (3i + 4j + 12k)/ √(3² + 4² + 12²)
u = (3i + 4j + 12k)/13

l=3/13

m=4/13

n=12/13

Thus, direction cosines of the corresponding vector are l = 3/13, m = 4/13, and n=12/13

Direction cosines as component of a unit vector on positive coordinate axes

For the vector v in consideration above, we get the unit vector  u = v||v||  and its components on positive coordinate axes as:

• Component on x-axis: ||u||cos(α) = cos(α) = l
• Component on y-axis: ||u||cos(β) = cos(β) = m
• Component on z-axis: ||u||cos(γ) = cos(γ) = n
  (since the magnitude of a unit vector is 1)

Thus, we can take direction cosines of a vector as its unit vector’s component on the positive coordinate axes.

The direction cosines of a vector is related to its unit vector. That means the magnitude of that vector isn’t used. This fact makes a mathematical conclusion that all vectors lying parallel to vector v (or coincident) have the same direction cosines.

Sum of squares of direction cosines of a vector

Using the Pythagoras theorem, it can be proved that the sum of squares of direction cosines of a vector is evaluated as unity.

Or, symbolically, we can say that:

cos²(α) + cos²(β) + cos²(γ) = 1

l² + m² + n² = 1

Supposing that the vector v is considered, and let (vx) = x component of v vector, (vy) = y component of v vector, and let (vz) = z component of v vector

then we get:

||v||² = (vx)² + (vy)² + (vz)²

Dividing both the sides by the square of length of the vector v, as from each positive coordinate axis’s view, we have the length of vector as hypotenuse, and the component as base, thus, we get square of cos trigonometric ratio, as shown below:

||v||²/||v||² = (vx)²/||v||² + (vy)²/||v||² + (vz)²/||v||²

1 = cos²(α) + cos2(β) + cos²(γ)

l² + m² + n² = 1

This property of the direction cosines is very useful. For example, if two of the direction cosines are known, the third missing direction cosine can be found using the equation we obtained above.

Direction ratios

The direction ratios are proportional numbers to the direction cosines of a vector.

For a vector v, if its direction cosines as l, m and n, its direction ratios are lk, mk, and nk, for any non-zero real number k.

Suppose the direction ratios are given, and we want to know the constant of proportionality used to form those ratios, then we can sum their squares and take their square root.

(lk)² + (mk)² + (nk)² = k²(l² + m² + n²) = k²

For the example discussed above, we had the direction cosine of the vector  v = 3i + 4j + 12k as:

l=3/13

m=4/13

n=12/13

If we take k = 13, then we get one pair of the direction ratios for the considered vector as:

a = lk = 3, b = mk = 4, and c = nk = 12

Conclusions

Direction cosines are cosines of the direction(angle) a vector makes with the positive coordinate axes. One other way to visualise direction cosine is to take them as the component of the unit vector of the considered vector’s direction on the positive coordinate axes.

The sum of squares of direction cosines of a vector equals 1.

Whereas, direction ratios are proportional numeric quantities to direction cosines. They are non-unique for a vector as there can be many proportional number pairs to the unique direction cosines of a vector.