Profile
Settings
Refer your friends
Sign out
An angle is the rotation measurement between two lines, including the type of rotation.
For a 3-dimensional Euclidean space, the rotation method of the terminal side to the initial side doesn’t matter as it depends on the point of reference. That is why there is no clockwise or anticlockwise angle in 3-dimensional Euclidean space unless a frame of reference is defined.
An Angle comes into existence when two lines are joined at a single endpoint, called vertex from which the angle is measured. One line, which is kept steady, is called the initial side. The other line, which rotates with the pivot being the vertex, is the terminal side.
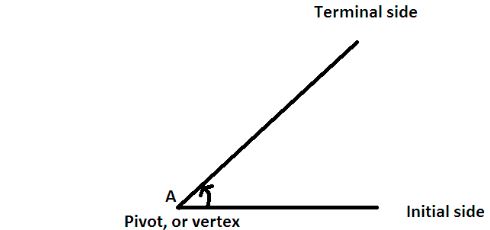
For three dimensional space, there can be two straight lines in place of these two lines.
Direction cosines of a vector
The direction cosines are cosines of the angle that the vector makes with the positive coordinate axes of the 3-dimensional Euclidean space.
Suppose there is a vector v in 3-dimensional Euclidean space ℝ³
Then the direction cosines of that vector are the component of the unit vector in the direction of v to the positive coordinate axes.
For considered vector, the unit vector in its direction is obtained as
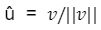
Where ||v|| is the magnitude of that vector. (It is the size of the vector).
Assuming the angles made by the vector with the positive coordinate axes are:
Angle between v and x-axis be α
Angle between v and y-axis β
Angle between v and z-axis be γ
Then, the direction ratios are defined as:
cos(α), cos(β), cos(γ)
They are usually written l, m, and n
Direction ratios
The direction ratios are proportional numbers to the direction cosines of a vector.
For a vector v, if its direction cosines as l, m and n, its direction ratios are lk, mk, and nk, for any non-zero real number k.
Equation of a line in three-dimensional Euclidean space
A straight line in a 3-dimensional Euclidean space is represented in many ways. One of the ways of representing it is using the direction ratios, as described above.
Suppose the considered three-dimensional line passes through the point
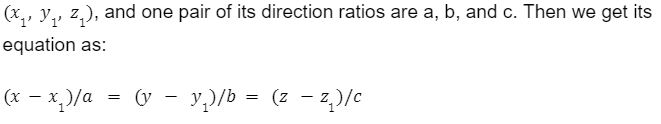
The angle between two line segments in a three-dimensional Euclidean space
The angle between two lines in 3-dimensional Euclidean space is the angle they make between each other. The lines may be skew but the lines will make some angle between them.
Another method (which we will use here) is the method of getting direction vectors in parallel to the lines and then measuring the angle between those two vectors whose endpoints are connected to the origin.
Suppose that the two lines given are:
Conclusion
The angle between two lines in a three-dimensional Euclidean space is the angle that they make with each other even if not touched. For measuring them, one method is to get the direction vectors parallel to them and then get the angle between them using the inverse cosine angle.
The angle between two lines in a three-dimensional world is different in the sense that there is no clockwise or anticlockwise angle as for them to be some entity, there has to be declared a frame of reference in the three-dimensional Euclidean space where lines are existing.
