Trigonometric identities
Trigonometric identities the relation between the angles of a triangle. These identities are used as the formula to solve trigonometric problems. There are three primary trigonometric identities, namely, sine (sin), cosine (cos) and tangent (tan). The relation between these three primary trigonometry identities is,
tanΘ=sinΘ/cosΘ
Three common trigonometry identities of the trigonometric function.
sin2Θ+cos2Θ=1
tan2Θ+1=sec2Θ
cot2Θ+1=cosec2Θ
Trigonometry equations
Trigonometric equations are those in which the trigonometric functions are present as variables. These equations can be solved using trigonometry identities and trigonometric functions.
Trigonometric ratios/functions of acute angles
Acute angles measure less than 90 degrees. All the angles lying in the first quadrant are acute angles.
Trigonometric ratios or functions of acute angles are the ratios of the set of sides of a right-angled triangle.
For a right-angled triangle ABC, the sides of the triangle are (a, b, c) shown below.
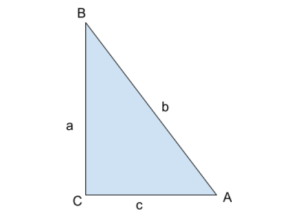
The six trigonometric functions for this triangle are,
Sine-
This function is the ratio of the opposite leg to a hypotenuse side.
sinA=a/c
Cosine-
This function is the ratio of the adjacent leg to a hypotenuse side.
cosA=b/c
Tangent-
This function is the ratio of the opposite leg to the adjacent side.
tan A=a/b
Cotangent-
This function is the ratio of the adjacent leg to the opposite leg.
cotA=b/a
Secant-
This function is the ratio of the hypotenuse leg to the adjacent leg.
secA=c/b
Cosecant-
This function is the ratio of the hypotenuse leg to the opposite leg.
cosec A=c/a
Values of different trigonometry functions at different acute angles are shown in the table.
A | sin A | cos A | tan A | cot A | Sec A | cosec A |
0° | 0 | 1 | 0 |
| 1 |
|
30° | 1/2 | 3/2 | 1/3 | 3 | 2/3 | 2 |
45º | 1/2 | 1/2 | 1 | 1 | 2 | 2 |
60º | 3/2 | 1/2 | 3 | 1/3 | 2 | 2/3 |
90º | 1 | 0 |
| 0 |
| 1 |
Here 0º and 90º is not the acute angle.
Example
The opposite leg, adjacent leg and hypotenuse sides of a right angle triangle are 1, 1 and 2 cm long respectively. Find the values of all trigonometry functions of the acute angle of 45º.
Solution:
Given;
Adjacent leg (a)= 1cm
Opposite leg (b)= 1cm
Hypotenuse side (c) = 2 cm
Angle =45º
Put the values in trigonometry functions for acute angle =45º.
i) sin(45º)=b/c=1/√2
ii) cos(45º)=a/c=1/√2
iii) tan(45º)=b/a=1/1=1
iv) cot(45º)=a/b=1/1=1
v) sec(45º)=c/a=√2/1=2
vi) cosec(45º)=c/b=√2/1=2
These values are true for the table shown above.
P is an acute angle such that 4/6. Find the value of sine, cosine and tangent functions.
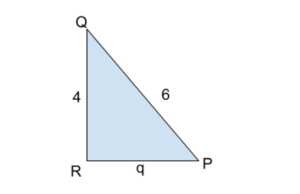
Solution:
Given:
QR=4
QP=6
PR=q
The value of q from the pythagorean theorem can be given as,
q2=62-42
q=36-16
q=10
Put the values in trigonometry function as,
i) sin(P)=opposite/hypotenuse=4/6=2/3
ii) cos(P)=adjacent/hypotenuse=√10/6
iii) tan(P)=opposite/adjacent=4/√10
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






