Profile
Settings
Refer your friends
Sign out
A triangle is a figure enclosed by three lines. A triangle consists of many properties based on its style of formation. But there are some certain things that apply to each and every triangle irrespective of its way of formation. Be it isosceles triangle or equilateral triangle, right angled triangle or acute angled triangle, these properties are applicable to all the triangles. Triangle has some specific properties that are useful in many areas of mathematics. We also use its applications in science and research. The area of triangle plays crucial role always. The circle definition has a part to play here.
Body
Triangle possesses a lot of properties which make them unique among all geometrical structures.
Property 1- If the two sides of a triangle are not equal, the angle formed in front of the longest side will be the biggest.
It means that, in a triangle that has two unequal sides, there will be an angle bigger than the remaining two angles. This angle, which is the biggest among all, will be positioned in front of the largest side. We can see this property right here-
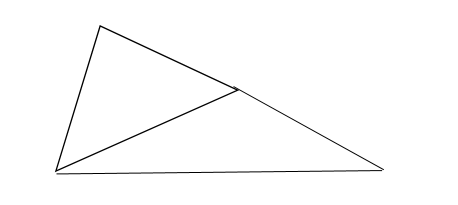
In this figure, we can see that in triangle ABD, AD > AB
Now, we make a new point C in the middle of the line AD such that AB = AC, and add point C to point B making the line BC.
In triangle ABC, AB = AC,
∠ 1 = ∠2 ( because similar sides have similar angles ) …..equation 1
∠2 is the exterior angle for triangle BDC.
∠2 > ∠ADB …. equation 2 ( by exterior angle theorem)
(exterior angle theorem says that the exterior angle is greater than either opposite interior angle)
From the equation1 and 2,
∠1 > ∠ABD
But we know that, ∠ABD > ∠1
So, ∠ABD > ∠ADB
Here, we see that if the two sides of a triangle are not equal to each other, the largest angle always lies in front of the largest side.
Property 2- If we draw a circle inside area of a triangle in a way that it touches all the three lines of that triangle, it is called the incenter of that triangle. The circle is based on circle definition. This also means that the three sides of the triangle are actually the tangents of the respective sides of the triangle. We also apply the circle definition here.
We can see this in following figure-
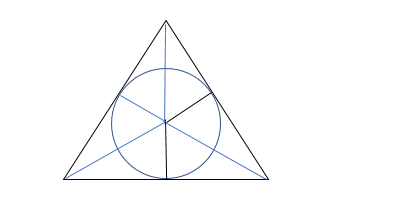
Here the circle is as per the circle definition. It has the same distance from the center evrywhere.
Property 3- In area of a triangle, the addition of two sides of a triangle is always greater than the third side of that triangle.
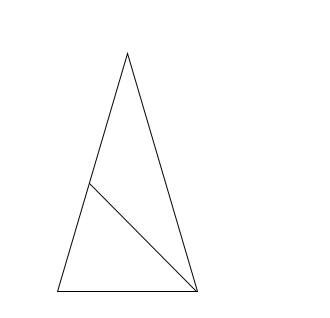
In this triangle, we see that in a triangle BDC, we extend the line BD to a point A and make a line BA.
In this triangle, DCA, DC = DA
So, ∠DCA = ∠ DAC (because same sides will have same angles also)
Now, ∠DCA + ∠BCD > ∠DAC
It simply means that, ∠DCA > DAC… equation 1
In triangle, BAC, ∠BCA > BAC
BA > BC …. equation 2
But BA = BD + DA = BD +DC…… equation 3
Now, be comparing equation 2 and 3,
BD + DC > BC
We can also say that, DB + BC > DC
And BC + CD > BD.
SO, whichever two sides we take, we always find the sum of two sides bigger than the third side of the triangle.
Property 4- A very interesting property of triangles is associated with triangles. It says that if we take a line segment, we take some point in the plane, which is not situated on that line segment. If we draw so many lines from that point to that line segment, the smallest line will be the perpendicular line only.
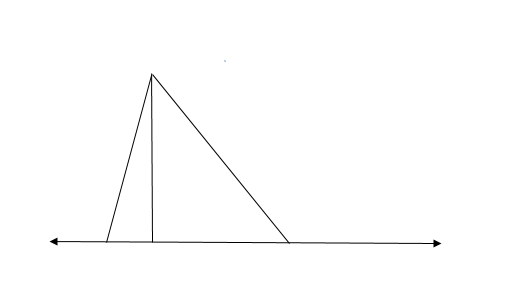
Conclusion:
We see that some common properties of the area of a triangle are applicable to all. The angle in front of the largest side, is the biggest one. The addition of two sides of a triangle always exceeds the length of the third side of the triangle. If we throw a perpendicular on a line segment from a point which does not lies on that line, that perpendicular will be the shortest line segment as all other lines thrown from the point to the line segment will be like the hypotenuse and this makes all the lines longer than the perpendicular one. We also saw the circle definition here.
