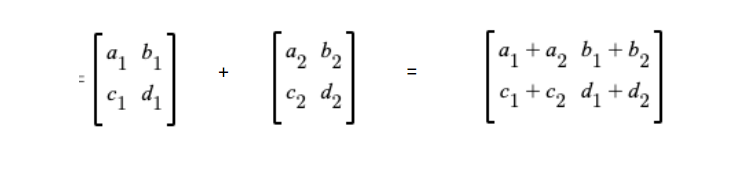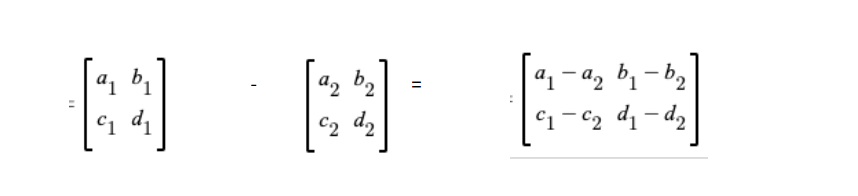Position of Specific Entry Matrices

A matrix is a rectangular sequence of numbers with rows and columns arranged in a grid. A matrix is represented by the array of numbers below.  

The dimension or order of a matrix refers to the number of rows and columns it contains. By practice, rows are listed first, followed by columns. As a result, we may state that the above matrix’s dimension (or order) is 3 x 4, implying that it has 3 rows and 4 columns.

The numbers that occur in the columns and rows of a matrix are referred to as matrix elements. The first column of the first row in the aforementioned matrix has the value 21; the second column of the first row has the value 62; and so on.

Notation in Matrix:

Symbols are used by statisticians to designate matrix elements and matrices.

Elements of the matrix: 

Consider the matrix below, where the matrix members are totally represented by symbols.                            

The first subscript, by convention, refers to the row number, while the second subscript refers to the column number. As a result, A11 represents the 1sts element in the first row. A12 represents the 2nd element in the first row. And so on, until we reach A24, the 4th element in the second row.

Matrices

There are various ways to symbolically portray a matrix. The most straightforward method is to utilise a boldface letter such as A, B, or C. As an example, A may indicate a matrix that is 2 x 4, as seen underneath.

• A = [Aij], where 1, 2 denotes I and 1, 2, 3, 4 is denoted by and j. This is another method of encoding matrix A.

• A is a matrix having two rows and four columns, as indicated by this notation. The array’s actual elements are not shown; instead, they are denoted by the Aij symbol.

Operations in a Matrix

Adding, subtracting, and multiplying matrices are the three most common operations in matrix operations. Mathematicians use matrices all the time in their work.

Each matrix must have exactly the same number of columns and rows as its neighbouring matrix if they are to be added or subtracted, and this is true for both multiplication and addition.

• Adding Matrices together

• Matrix Subtraction 

• Scalar Matrix Multiplication

• Mathematical Matrix Multiplication

Adding Matrices together:

The matrix sum of A[aij]mxn and B[bij]mxn is a matrix with each element equivalent to the sum of the elements of the two matrices. For example, the sum of A and B is [aij+bij]mxn.

Assume A and B are two 2 x 2 matrices. The final sum is as follows:

Matrix Addition Properties:

If A, B, and C are all matrices of the same order, then the properties of matrix addition are the same.

(a) Commutative Law: A + B Equals B + A. 

(b)  The Associative Law is: (A+B+C) – C = A+(B+C).

(c) Matrix identity: A + O = O + O = A, where zero matrix is denoted by O and the matrices are additively identical.

 (d) Additive Inverse: It’s possible to get (-A) by flipping the signs of all of A’s elements that are additive inverses of the matrix. The formula is A + (-A) = 0 = (-A) + A

If A + B and B + A = 0, then B is the additive inverse of A and A is the additive inverse of A.

Matrix Subtraction:

If A and B have the same order, then A-B = A+ (-B)

Assume A and B are two 2 x 2 matrices. Therefore, the difference can be calculated as follows:

Subtracting each member of one matrix from its corresponding element in the second matrix allows us to subtract the matrices. 

Therefore, the value of A-B can be derived from [aij – bij]mxn.

Multiplying Matrices by Scalars:

If A= [ a ij  ] mxn is a matrix and k is any number, the scalar multiplication of A by k is called k A 

thus, if A=  a ij      mxn   is a matrix, then:

KA mxn  =    Am x Nk = [ Ka ij]

Mathematical Matrix Multiplication:

No matter how many rows or columns there are in A and B, their product AB will be determined if their numbers are equal.

Matrix Multiplication Properties

• Commutativity is not guaranteed in matrix multiplication, hence, AB does not always equal BA. 

• It is associative to multiply matrices in the sense that (AB)C = A (BC).

• A.(B + C) = A.B + A.C and (A + B)C = AC + BC is a distributive matrix multiplication.

• ImA=A=AInif A is An  mxn matrix.

• When two matrices are combined, the product of the two matrices can be a null matrix when neither of the matrices is a null matrix. So, if AB=0 then it does not mean that either A or B has to be 0. 

• When A is an mxn matrix and O is a null matrix, then, Amxn. Onxp=Omxp 

• Even if A and B may not be equal to zero, the product of their matrices may be zero.

• If AB is equal to AC, then B is equal to C. (Cancellation Law doesn’t apply here).   

• tr (BA)= tr (AB) 

• For any square matrix, there exists a multiplicative identity such as AI=IA=A             

Conclusion

We have learned about the matrices, their notation, their operations and different properties with examples. We have also covered addition, subtraction, and multiplication operations. Here are some of the basic points to remember:

• An arrangement of numbers, expressions, or symbols, arranged in rows and columns is known as a matrix (plural: matrices).

• As the name suggests, the matrix dimensions are the number of rows and the number of columns.

• Multiple linear equations, or a system of linear equations, can be written and solved using matrices. When applied to linear transformations, or linear maps, matrices and matrix multiplication show their fundamental characteristics.