Profile
Settings
Refer your friends
Sign out
Inverse trigonometric functions are simply the inverses of the basic trigonometric functions, namely, sine, cosine, tangent, cotangent, secant, and cosecant. The formulas of multiple angles of these trigonometric functions can also be expressed in the form of their inverses. We know that the values of multiple angles cannot be obtained directly. But, we can find the values by expanding each trigonometric function to its lowest multiple. The same rule is applicable even in the case of inverse trigonometric functions.
In order to find a certain angle with the help of trigonometry ratios, we use the inverse trigonometric functions. Before we learn about multiple angles in terms of sin-1x and cos-1x,let us discover their general and principal values.
General Value and Principal Value of Sin-1x :-
General Value and Principal Value of Cos-1x :-
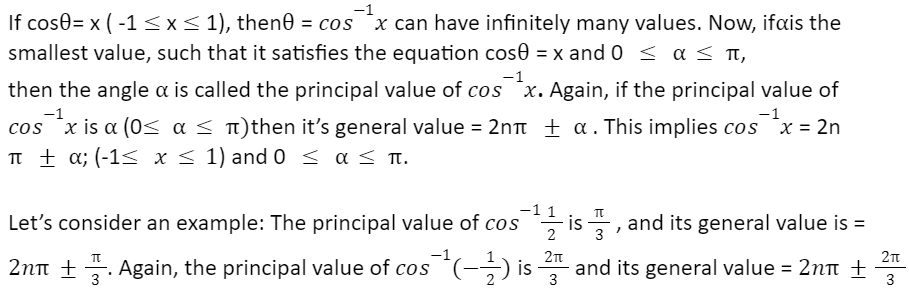
Now let’s learn to prove the various multiple angles in terms of sin-1x and cos-1x:
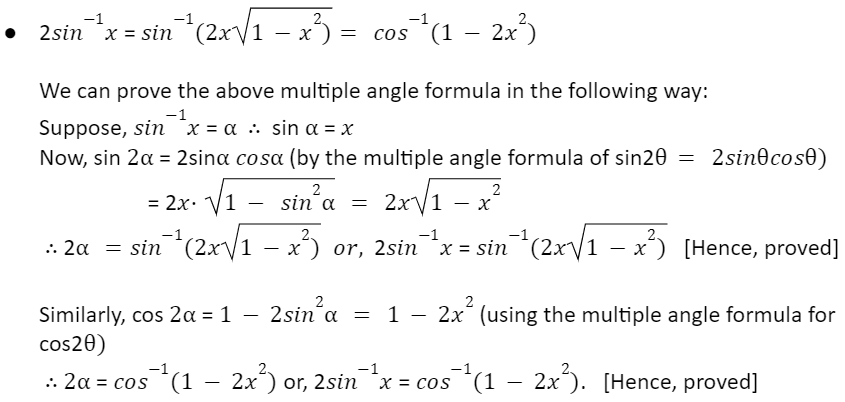
Conclusion
Multiple angle formulas are formed with the help of trigonometric functions. Here, we learnt to apply these formulae in the case of inverse trigonometric functions. Be mindful not to confuse the inverse trigonometric function sin-1x with (sin x)-1, which means 1/sin x= cosec x. In the above segment, we learned that the smallest positive or negative value is called the principal value of the trigonometric function. Moreover, any possible value of the function can be expressed in the same form, known as the general value.
The multiple angles in terms of sin-1x and cos-1xcan be obtained by using the multiple angle formulae of sin x and cos x.
