Profile
Settings
Refer your friends
Sign out
No matter what sign the number has, a modulus function gives its magnitude. This function is also referred to as the absolute value function. A modulus function is a way to determine the modulus of any real number x, denoted by | x |. A modulus function returns a nonnegative value for x. Numbers are also known by their modulus or absolute values, which can be viewed as distances from the origin or zero. From a geometric perspective, the absolute value represents an absolute displacement from the origin (or zero) and is therefore nonnegative. If the value of a real number a is positive or zero, then its absolute value is itself. An absolute value is not just used to graph a number’s distance from the origin, but also to represent the number’s value from the origin.
Formula of Modulus:
y = |x| or f(x) = |x|, where f: R → R and x ∈ R.
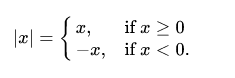
Hence, when x is greater than or equal to 0, then the modulus function will calculate the actual value, and when x is less than 0, then the function will calculate the minus of the actual value.
The modulus of x is |x|, where x is a real number. In case x is non-negative, then f(x) will also have a similar value to x. In the case of a negative x, then f(x) will be the magnitude of x, that is, f(x) = -x in the case of a negative x.
Properties of Modulus:
- It is only possible for x = 0 if |x|= 0. From a mathematical perspective, |x| = 0 if x = 0.
- The value of x is always non-negative, i.e. |x| is 0, regardless of x. Due to the fact that |x| denotes distance, something that can never be negative. That follows naturally from the definition. If x ≥ 0, then |x| = x, the equivalent would be |x| ≥ 0. If x < 0, then |x| = –x. It follows that |x| > 0 in this case as well.
- The value of |x| = |–x| for all values of x.
- Other Important properties:
- Absolute value of the absolute value is idempotence (absolute value of absolute value), ||a||=|a|
- Symmetry |−a|=|a|
- Identifiability of indiscernibles (equivalent to certainty), |a−b|=0⇔a=b
- Triangular inequality (equivalent to subadditivity), |a−b|≤|a−c|+|c−b|
- Maintaining division (equivalent to multiplying), |a/b|=|a|/|b| if b≠0
- equals (subadditivity), |a−b|≥||a|−|b||
Absolute value function (modulus) relationship to the sign function:
Regardless of what the input is, a modulus function will always produce a positive output. Absolute value functions of real numbers return their value regardless of their sign, whereas sign (or signum) functions return the number’s sign regardless of its value.
Derivative of Absolute value function or modulus function:
Real absolute value functions are examples of continuous functions that achieve a global minimum at which there are no derivatives. In the case of x = 0, the subdifferential of |x| is [−1, 1].
Anti-derivative of Absolute Value Function:
Absolute values do not have an antiderivative; nevertheless, the definition is known. Therefore, we can split up our integral in accordance with whether x3 − 5×2 + 6x is non-negative. In the real absolute value function, the antiderivative (indefinite integral) is:
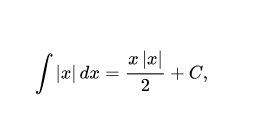
where C is an arbitrarily chosen integration constant. It can’t be a complex antiderivative because complex antiderivatives can only be derived from complex-differentiable (holomorphic) functions, which is not the case here.
Modulus of a number:
In mathematics, modulus refers to the absolute size of a number. Therefore, the modulus of a positive number is simply the number itself. Despite the minus sign, you can find the modulus of a negative number. By writing vertical lines around a number, we denote the modulus of that number. Additionally, the modulus of a negative number may be found by multiplying it by 1 since, for example, −(−8) = 8.
Conclusion:
In mathematics, the modulus is one of the most important tools. In all cases of positive or negative numbers, the modulus function, also called the absolute value of the function, provides the magnitude, or total value. Any number or variable provided by the modulus functions will never be negative. An absolute value describes how far away a number is from zero. With a negative number, simply drop the sign, and the absolute value will be that number; with a positive number, the absolute value is what the number is. As a result, the absolute value of a number is always positive.
