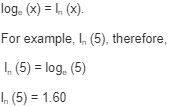Logarithms and their Applications

Logarithms are a way of looking differently at the exponential or indices. A logarithm is based on the two Greek words: logos and arithmos. In this scenario, we could translate it as “ratio” or “proportion”. John Napier invented the word ‘logarithms.

This material speaks about logarithms and their applications. You will find brief information on the concept of logarithms, a thorough explanation of properties of logarithms, applications of logarithms, and so on.  So, let’s, start with the definition of logarithms.

Definition of Logarithms

A logarithm is defined as the base that must be raised to an exponential or power to fetch the given number.

Any positive real number N, can be expressed in two ways – 1) exponential and 2) logarithmic presentation. For example, N = 25, this can be written in exponentially as 25 = 5², and the same can be expressed as logarithmic function as log₅ 25 = 2; thus we could say log of a number ‘N’ to a given base ‘a’ is the exponent ‘x’, by which the base must be raised in order to get ‘N’ i.e.,

Log_a N = X ⇔ N = ax , where N > 0, a > 0 and a ≠ 1.

For example, 2⁴= 16; therefore, 4 is the log of 16 to the base 2, or 4 = log₂ 16.

Types of Logarithms

Types of logarithms are divided based on the base of logarithms into common logarithms and natural logarithms accordingly. Let’s walk through these types of logarithms in more detail.

1. Common Logarithm

A common logarithm is defined as the logarithm function with base 10. Common logarithm mathematically be defined as, log10 (x) = log (x) .

For example, log (10000) = 4

2. Natural Logarithm

A natural logarithm is defined as the log function with base ‘e’, where ‘e’ is the constant value. This can be mathematically expressed as loge (x), where the value of ‘e’ = 2.71828. That means it defines how many times we have to multiply the ‘e’ to get the expected output. This can also be written as

 Rules of Logarithms

1. Multiplication Rule

The product of two logarithms value is equal to the sum of their individual logarithm.

2. Division Rule

The division of two logarithmic functions equals the subtraction of their individual logarithms.

3. Power Rule

The log of ‘X’ to the power ‘n’ with base ‘a’ will exactly be the same as ‘n’ times of log ‘X’ to the base ‘a’

4. Change of Base Rule

In the change of base rule, the shifting of a base from b to c, can be achieved through logarithm of ‘x’ to the base ‘b’ is equal to logarithm of ‘x’ to the base ‘c’ divided by logarithm of ‘b’ to the base ‘c’.

Applications of Logarithms

A logarithmic scale is used as a tool to deal with a large range of values. The common application of the logarithmic function is to find the compound interest, exponential growth, and decay, to find the pH level of substance, to know the magnitude of an earthquake, etc.

Logarithms are used to know the magnitude of earthquakes.

Logarithmic functions are used to measure the pH level of chemicals where pH = log10 [H+].

The exponential growth can be measured using the logarithmic functions.

For example, the money growth rate at a given fixed interest rate can be determined.

For example, you have Rs.40,000 in your bank account at an interest of 4%. With a logarithm, you may know when your money will reach Rs.42,000.

Logarithms are used in specific calculations where multiplications are converted into additions.

Logarithms are used to determine radioactive decay.

Basic Properties of Logarithms

1. Log of 1 to any base will always equals 0. This could be expressed as logb 1 = X.

For example, log81 = 0; log2001 = 0 etc.

2. Log of ‘b’ to the base ‘b’ will be equal to 1, i.e., if the argument and the base are the same,  then the logarithm will be 1. i.e., logb b = 1.

For example, log2 2 = 1.

3. Log of ‘b’ raised to ‘n’ to the base ‘b’ will be ‘n’. This function can be written as logbbn = n.

For example, log13134 = 4.

Conclusion

In this article describing the logarithms, we studied the concept of the logarithms in broader detail. We covered several other topics such as the definition of logarithms, properties of logarithms, rules of logarithms, applications of logarithms, and other related topics along with the solved examples. We hope you find this study material helpful for a better understanding of logarithms and their applications.