Profile
Settings
Refer your friends
Sign out
Calculus is a branch of maths that deals with calculations of values that are ever changing. Limits are one of the key concepts. Limits are an analysis done on how the function behaves near a given point. The limit formula is also discussed below. Continuity and differentiation also employ the limit formula. Some properties of limits are discussed below.
What is calculus?
Calculus is a branch of mathematics that involves dealing with calculations around whose values keep differing or changing.
What is the limit of a function?
One of the fundamental concepts in calculus is the limit of a function. Limit of a function is defined as an analysis that is done on the way the function behaves around or near to a given input.
The first formal definition was noted and written down around the early years of the 19th century. When a function, k is assigned an output k(x) to an input of every x. We notice that the function has L as the limit at an input, y, if the k(x) moves very close gradually to L as the value of x moves gradually closer to the value of k.
What is the use of the limit of functions?
Modern calculus finds the use of the applications of limits. The concept of continuity and differentiation make use of limits: the function is continuous only when all the limits are equal to values of the function. Limits also find its mention in defining what is a derivative: where it is the value of secant line slope of the graph of the given function.
What is the limit formula?
As mentioned before, understanding the concept of limits is very important as it forms a base for other topics like differentiation, continuity, etc.
When k= f(x) acts as a function of x, at any given point let’s say x= p, f(x) is of indeterminate form, then we can say that values of function x are close to p.
lim f(x)=L
x→p
The above given formula is the limit formula where lim stands for limit.
Limit formula can be read as ‘the limit of a given function f of x as x nears p is L.’
Properties of Limits
Like there are algebraic identities, they help us solve complex problems similarly properties of limits involving the limit formulas help us easily solve a group of problems. I’ll be discussing seven of them here. Let’s understand them in detail with the help of their formulas:
1.The Notation of a Limit
lim f(x)=L
x→p
This denotation of f(x) L and x p is called the limit notation. It means that the limit is moving from the value of f(x) to L and x to p.
2. The sum rule
For the next rules we make an assumption that there exists such a function;
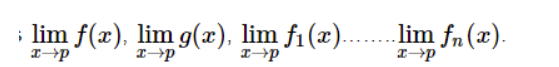
Now the sum rule states that the addition of any two functional limits yields the same limit as the sum of all other limits.
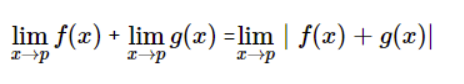
3.The extended sum rule
Just like the sum rule, the only differing property is that it is used for more than two functional limits.
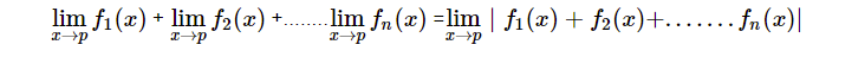
4.The constant function rule
This property states that the limit of any constant function is always a constant.
5.The product rule
Just like the sum rule, this states that the product of any two functions yields the limits of all the functions.
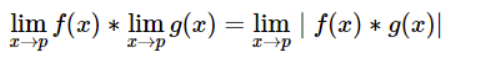
6.The quotient rule
When the limit of the denominator is not equal to zero, the quotient of individual limits of two functions equals the limit of the quotient of the two functions when the functional denominator is zero.
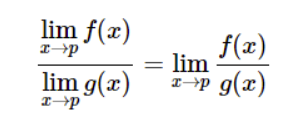
7.The power rule
The rule cannot be defined in words but the following is it’s mathematical interpretation:
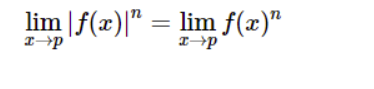
Conclusion
Calculus is an important part in maths especially when it comes to its real life applications in physics and chemistry. Limits are an analysis done on how the function behaves near a given point. The limit formula is also discussed above. Continuity and differentiation also employ the limit formula. A few of the properties based on limit formulas are also discussed.
