Profile
Settings
Refer your friends
Sign out
Trigonometry is a vast field with a lot of diverse and interesting topics. Here we shall focus on one such topic which is inverse trigonometry. Firstly, one can also refer to inverse trigonometric functions as anti-trigonometric functions as well as arcus functions. Inverse trigonometry is used for solving those questions in which we can’t recall the answers as well as are unable to solve using a calculator. For example, if a question like this comes up –
Y = SinX then one can find its solution by either using a calculator or remembering what the answer was. However, imagine the question is X = Sin(Y)? Now, in such a question the input shall be a number but one needs to figure out the angle whose sine is equal to that digit. Thus, it is in situations like these that we can make use of inverse trigonometry.
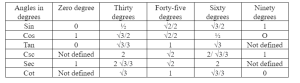
Trigonometric Table
For finding the ratio for certain angles such as zero-degree, sixty degree etcetera one can refer to a trigonometric table. Thus, the table comprising of trigonometric ratios can be called as a trigonometric table. Here is the depiction of a trigonometric table in the sexagesimal system:
Inverse Trigonometry Function
An inverse trigonometric function can be explained as an inverse relation wherein the range can be confined. The inverse trigonometric functions and the inverse relations are similar in terms of their names however the difference is such that the functions begin with a capital letter. For example, if Arcsine is a function then arcsine shall be the relation.
The inverse trigonometric relations are as mentioned below –
Sine – arcsine
Cosine – arccosine
Tangent – arctangent
Cosecant – arccosecant
Secant – arcsecant
Cotangent – arccotangent
Thus, these are the various inverse trigonometric relations for cotangent, secant, cosecant, tangent, cosine and sine.
One more way through which it can be expressed is like –
X = Sin(Y) can be equal to Y = Arcsine(X)
Here are few trigonometric formulae listed which can help in better understanding about the concept-
1.Arctangent – y = arctangent of x = arctan(x) = tan-¹(x) which can also be written as
x = tan(y)
2.Arcsecant = y = arcsecant of x = arcsec(x) = sec-¹(x) which can also be written as
x = sec(y)
3.Arccosine = y = arccosine of x = arccos(x) = cos-¹(x) which can also be written as
x = cos(y)
4.Arccosecant = y = arccosecant of x = arccsc(x) = csc-¹(x) which can also be written as x = csc(y)
5.Arcsine = y = arcsine of x = arcsin(x) = sin-¹(x) which can also be written as x = sin(y)
6.Arccotangent = y = arccotangent of x = arccot(x) = cot-¹ (x) which can also be written as x = cot(y)
Uses of Inverse Trigonometric Functions
Arcus functions which can also be called anti/trigonometric functions or inverse trigonometric functions have multiple uses in trigonometry. These uses are listed below –
- Inverse trigonometric functions can help one in finding out the angles accompanied by some trigonometric ratio.
- Adding on to the first point, inverse trigonometric functions are also helpful in various fields such as engineering, geometry etcetera.
Thus, these two uses shed light on the importance of inverse trigonometric functions.
Conclusion
As observed from the above different sections, it can be said that the trigonometric table and trigonometric formulae are now clearly understood. The various inverse relation of trigonometry along with their uses are also discussed in detail. Thus, it can be concluded that various concepts regarding the inverse relation of trigonometry have been clearly mentioned in a comprehensive manner.
