Profile
Settings
Refer your friends
Sign out
The study of the relationship of and between angles, heights, and lengths is known as Trigonometry. This field of study is used in several other fields of study, like- astronomy, oceanography, geography, engineering, criminology, architecture, etc. the functions of trigonometry are the functions of the angles of the triangles. The relationship between the sides of the triangles and the angles of the triangles are given out by the functions of trigonometry. Therefore, there are six fundamental trigonometric functions. These functions are Cosecant, Secant, Cotangent, Tangent, Cosine, and Sine.
The angles that are most commonly used in trigonometric problems and sums are 90, 60, 45, 30, and 0 degrees. Each of these angles, with respect to the trigonometric functions, have different values- which are easier to memorize. Through these basic angles, it is possible to calculate other major angles of trigonometry. In addition to this, the measure of a triangle involves inverse trigonometric functions. These functions can be said as Sin of 1, Cos of 1, Tan of 1, etc. Another name for this inverse function is known as the Arcus function.
Now, let us look at the domain and principal values of the several inverse functions of trigonometry.
Domain and Principal Values
The principal value of a trigonometric function is the value of an inverse function at a certain point. This point falls within the range of the principal unit value. Let us look at the domain of these inverse trigonometric functions-
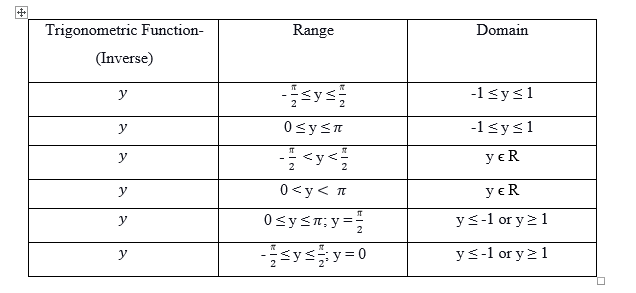
Now, let us look at the value for tan of 1, tan inverse 1, and inverse tan of 1, among all six fundamental functions of trigonometry.
Inverse Tan
The inverse of the trigonometric function of Tan is known as the Inverse tan. This is written as y . This is also known as “arctan”. And, when the value of “y” is taken as unitary, it can be written as 1 or Tan inverse 1. We will discuss the tan of 1, in addition to its properties. For instance, when the two functions are an inverse of one another, then if f (y) = z and z = y . Therefore, when the function” tan” moves from one side of the equation to another, then it turns to be . Let us see how the tan inverse works.
Tan π ⁄ 4 = 1 => 1 = π ⁄ 4
The inverse of the tan trigonometric function can be used to find the angles of a right-angled triangle. This is possible only when the values of the opposite and adjacent side of the triangle is given.
Here, the tan inverse 1 will be π ⁄ 4. That is, moving tan to the other side of the equation. Now, let us briefly look at two special cases of tan- tan of 1 and tan of 1 (negative).
Tan of 1s
The tan of 1 and tan of 1 (negative) are the two special cases of the inverse of trigonometric function tan. It must be noted that the tan of 1is the angle that has a tangent value of 1.
We know that ,
Sinθ ⁄ Cosθ = Tan θ
Therefore, the value of Sin θ and Cos θ is the same at 4 angle, that is 45 degree angle. Hence, that value of tan also becomes unitary. We can generalize the following identity:
1 =π ⁄ 4 + 2 π g
Here, g is an integer.
Conclusion
The study of the relationship of and between angles, heights and lengths is known as Trigonometry. This field of study is used in several other fields of study, like- astronomy, oceanography, geography, architecture, etc. there are six fundamental trigonometric functions. These functions are Cosecant, Secant, Cotangent, Tangent, Cosine, and Sine. The angles that are most commonly used in trigonometric problems and sums are 90 degree, 60 degree, 45 degree, 30 degree, and 0 degree. There are radian measure for these degree measure. The inverse of the trigonometric function of Tan is known as the Inverse Tan. This is written as the y . This is also known as “arc tan”. The tan of 1 and tan of negative 1 are the two special cases of the inverse of trigonometric function tan. It must be noted that the tan of 1is the angle that has a tangent value of 1.
